TÍNH GIÁ TRỊ BIỂU THỨC
P= sin2 200 + sin2 400 + sin2 450 + sin2 500 + sin2 700
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Từ giả thiết ta suy ra:
B = tan2x (sin2x - 1) + sin2 x = -tan2x.cos2x + sin2x
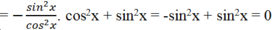

Lần sau bạn vào cái hình E để gửi câu hỏi nha!
\(P=\dfrac{sin^2\alpha-sin\alpha\cdot cos\alpha+2cos^2\alpha}{2sin^2\alpha-cos^2\alpha}\)
\(P=\dfrac{tan^2\alpha-tan\alpha+2}{2tan^2\alpha-1}\) (Chia cả tử và mẫu cho \(cos^2\alpha\))
\(P=\dfrac{3^2-3+2}{2\cdot3^2-1}=\dfrac{8}{17}\)
Chúc bn học tốt!

\(P.sina=\dfrac{sina}{sin2a.sina}+\dfrac{sina}{sin3a.sin2a}+...+\dfrac{sina}{sin\left(n+1\right)a.sinna}\)
\(=\dfrac{sin\left(2a-a\right)}{sin2a.sina}+\dfrac{sin\left(3a-2a\right)}{sin3a.sin2a}+...+\dfrac{sin\left[\left(n+1\right)a-na\right]}{sin\left(n+1\right)a.sinna}\)
\(=\dfrac{sin2a.cosa-cos2a.sina}{sin2a.sina}+\dfrac{sin3a.cos2a-cos3a.sin2a}{sin3a.sin2a}+\dfrac{sin\left(n+1\right)a.cosna-cos\left(n+1\right)a.sinna}{sin\left(n+1\right)a.sinna}\)
\(=cota-cot2a+cot2a-cot3a+...+cot\left(na\right)-cot\left(n+1\right)a\)
\(=cota-cot\left(n+1\right)a\)
\(\Rightarrow P=\dfrac{cota-cot\left(n+1\right)a}{sina}\)

Sử dụng 2 công thức: \(sina=cos\left(90^0-a\right)\) và \(sin^2a+cos^2a=1\) ta có:
\(A=sin^25^0+cos^2\left(90^0-85^0\right)=sin^25^0+cos^25^0=1\)

Đáp án B
Theo giả thiết có 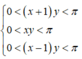 và
và
![]()

Và thay vào đẳng thức điều kiện có:
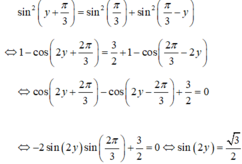
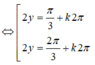
Đối chiếu với điều kiện nhận 

\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)

P=sin2200+sin2400+sin2450+sin2500+sin2700
đổi sin2500 thành cos2400,sin2700 thành cos2200 rồi thay vào ta được:
sin2200+cos2200+sin2400+cos2400+\(\left(\dfrac{\sqrt{2}}{2}\right)^2\)
=\(2+\dfrac{1}{2}=\dfrac{5}{2}=2,5\)