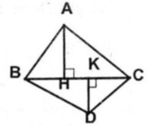
Qua điểm o lẩy trên đường cao BH cùa A ABC kỏ các đường thẳng AO và CO, chúng cắt các cạnh Be và BA tương ửní> lại các điểm K và M. Chứng minh rằng KHB - MHB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 11 2017
Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC
CM
26 tháng 3 2017
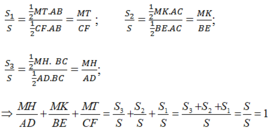
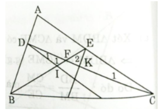
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
Tương tự ta có: ΔDFB ∼ ΔKFE
Từ (1), (2) ⇒ FC.FI = FB.FK
Do đó theo định lí Talét đảo ta có KI // BC.
22 tháng 11 2015
EG+ FH= AB
<=> EG/AB+ FH/AB = 1
Áp dụng tính chất đoạn thẳng tỷ lệ, ta có:
FH/AB= CF/BC
EG/AB =CE/BC=(CF+FE)/BC
= (CF + BC - 2CF)/BC=(BC-CF)/BC = 1- CF/BC
Vậy EG/AB+ FH/AB =1- CF/BC + CF/BC =1
4 tháng 1
Giải thích các bước giải:
a.Ta có xy//BC,MD//AB��//��,��//��
→AD//BM,AB//DM→ˆBMA=ˆMAD,ˆBAM=ˆAMD→��//��,��//��→���^=���^,���^=���^
Mà ΔABM,ΔMDAΔ���,Δ��� chung cạnh AM��
→ΔABM=ΔMDA(g.c.g)→Δ���=Δ���(�.�.�)
→AD=BM,MD=AB→��=��,��=��
Tương tự chứng minh được AE=MC,ME=AC��=��,��=��
→DE=DA+AE=BM+MC=BC→��=��+��=��+��=��
→ΔABC=ΔMDE(c.c.c)→Δ���=Δ���(�.�.�)
b.Gọi AM∩BD=I��∩��=�
→ˆIAD=ˆIMB,ˆIDA=ˆIBM(AD//BM)→���^=���^,���^=���^(��//��)
Mà AD=BM��=��
→ΔIAD=ΔIMB(g.c.g)→Δ���=Δ���(�.�.�)
→IA=IM,IB=ID→��=��,��=��
Lại có AE//CM→ˆEAI=ˆIMC��//��→���^=���^
Kết hợp AE=CM��=��
→ΔIAE=ΔIMC(c.g.c)→Δ���=Δ���(�.�.�)
→ˆAIE=ˆMIC→���^=���^
→ˆEIC=ˆAIE+ˆAIC=ˆMIC+ˆAIC=ˆAIM=180o→���^=���^+���^=���^+���^=���^=180�
→E,I,C→�,�,� thẳng hàng
→CE,AM,BD→��,��,�� đồng quy
4 tháng 10 2015
Trên cạnh AB lấp điểm I sao cho BI = EG.
Nối IG.
Xét tứ giác IBEG có IB//EG và IB = EG nên IBEG là hình bình hành
=> IG//BC và IG= BE
Mà BE = CF nên IG = CF.
Vì IG//BC nên góc AIG = góc IBE mà góc IBE = góc HFC do HF//AB
=> góc AIG = góc HFC
Lại có góc AGI = góc HCF nên ta có tam giác AIG = tam giác HFC (g.c.g) => AI = HF
Ta có AB = BI + AI = EG + FH (vì A I= FH)