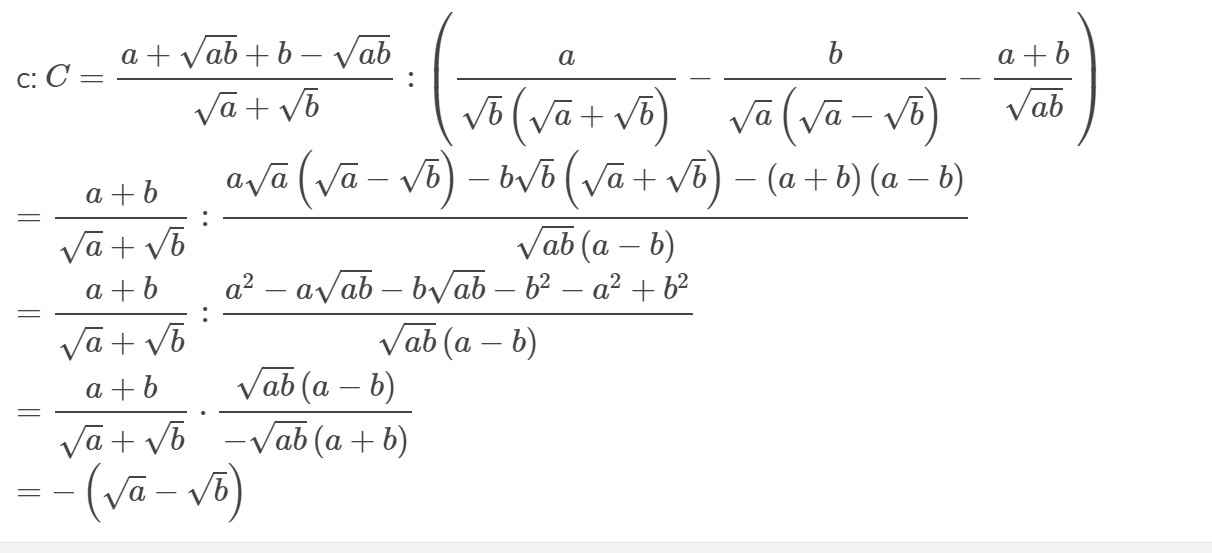Rút gọn biểu thức sau:
a) A= \(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\left(\dfrac{\sqrt{b}}{a-\sqrt{ab}}-\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\)
b) B=\(\left(\dfrac{2}{\sqrt{a}-\sqrt{b}}-\dfrac{2\sqrt{a}}{a\sqrt{a}+b\sqrt{b}}.\dfrac{a\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}\right):4\sqrt{ab}\)
giúp mình với ạ, mk cần gấp lắm