cho tam giác ABC, A=90 độ, B=51 độ, AB=2,8cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
Cho tam giác abc ( a=90 độ). giải tam giác vuông abc biết a)AB =30cm , acb=30 độ b) AB=20cm ;AC=13cm
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
a.
Trong tam giác vuông ABC:
\(tan\widehat{ACB}=\dfrac{AB}{AC}\Rightarrow AC=AB.tan\widehat{ACB}=30.tan30^0=10\sqrt{3}\left(cm\right)\)
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=20\sqrt{3}\left(cm\right)\)
\(\widehat{ABC}=90^0-\widehat{ACB}=60^0\)
b.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{569}\left(cm\right)\)
\(tan\widehat{ABC}=\dfrac{AC}{AB}=\dfrac{13}{20}\Rightarrow\widehat{ABC}\approx33^0\)
\(\widehat{ACB}=90^0-\widehat{ABC}=57^0\)
16 tháng 3 2023
3:
Đặt HB=x; HC=y
Theo đề, ta có: x+y=289 và xy=120^2=14400
=>x,y là các nghiệm của phương trình:
a^2-289a+14400=0
=>a=225 hoặc a=64
=>(x,y)=(225;64) và (x,y)=(64;225)
TH1: BH=225cm; CH=64cm
=>\(AB=\sqrt{225\cdot289}=15\cdot17=255\left(cm\right)\) và \(AC=\sqrt{64\cdot289}=7\cdot17=119\left(cm\right)\)
TH2: BH=64cm; CH=225cm
=>AB=119m; AC=255cm
9 tháng 5 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
MP
9 tháng 5 2023
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
NT
2
29 tháng 8 2023
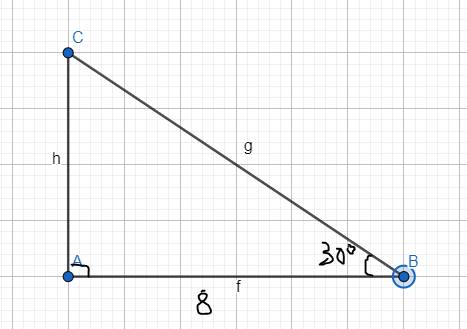
ΔABC vuông tại A
=>góc B+góc C=90 độ
=>góc C=60 độ
Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}\)
=>8/BC=căn 3/2
=>BC=16/căn 3(cm)
=>\(AC=\dfrac{8}{\sqrt{3}}\left(cm\right)\)
17 tháng 1 2022
tam giác ABC vuông tại A(vì ∠A=90 độ)
vẽ AD cắt BC tại D sao cho ∠ADB=60 độ
=> tam giác ABD đều(DHNB tam giác đều)
=>BD=AB=AD=3cm
tam giác ACD cân tại C vì ∠C= ∠DAC=30 độ
=> tam giác ADC cân tại D
=>CD=AD
mà AD=3cm (cmt)
=>CD=3cm
mặt khác BC=CD+BD(cv)
=>BC=CD+BD=3+3=6
=>BC=6cm
áp dụng định lí Pytago cho tam giác ABC vuông tại A ta có
BC^2=AB^2+AC^2
=>6^2=3^2+AC^2
=>36=9+AC^2
=>AC^2=25
=>AC=5
vậy AC=5,BC=6
9 tháng 5 2023
a: góc C<góc B
=>AB<AC
b: Xét ΔABM co AB=AM và góc A=60 độ
nên ΔAMB đều
góc C=90-51=39 độ
Xet ΔABC vuông tại A có sin C=AB/BC
=>2,8/BC=sin39
=>BC=4,45cm
=>AC=3,46(cm)