Khi nối trung điểm của 2 đá y hình thang tại sao ta được 2 hình thang có diện tích bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
4 tháng 10 2017
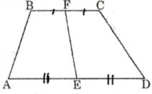
+) Vẽ hình thang ABCD như hình trên. Gọi E, F lần lượt là trung điểm của hai đáy AD BC.
Gọi h là chiều cao của hình thang ABCD. Khi đó h cũng là chiều cao của hình thang BFEA và hình thang FCDE.
+) Diện tích hình thang BFEA là:
+) Lại có: BF = FC (vì F là trung điểm của BC) (3)
AE = DE (vì E là trung điểm của AD) (4)
+) Từ (1); (2); (3) và (4) suy ra: SBFEA = SFCDE.
SG
1
21 tháng 4 2017
Cho hình thang ABCD. Gọi M, N lần lượt là trung điểm của hay đáy AB, CD. Ta có hai hình thang AMND và BMNC có cùng chiều cao, có đáy trên bằng nhau AM = MB, có đáy dưới bằng nhau DN = NC. Vậy chúng có diện tích bằng nhau.
22 tháng 1 2021
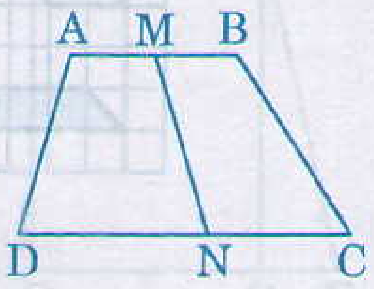
Giả sử hình bình hành ABCD có E, F lần lượt là trung điểm của CD và AB.
Ta có hai hình thang AFED và BFEC có cùng chiều cao, có đáy trên bằng nhau AF = FB, có đáy dưới bằng nhau DE = EC.
=> SAFED = SBFEC
QC
0
BO
14 tháng 1 2017
M là trung điểm CD nên DM = MC
AB = 1/2 CD nên AB = DM = MC
3 tam giác AMD; AMB, BCM cùng có chung 1 đường cao với hình thang ABCD; và có đáy AB = DM = MC
Nên 3 tam giác này có diện tích bằng nhau
S(ABCD) = S(AMD) + S(AMB) + S(BCM)
Diện tích hình thăng ABCD :
35 x 3 = 105 m2
29 tháng 5 2023
Giải
- Độ dài đoạn MB=1/3 đoạn AM vì MA=2/3 AB suy ra đoạn MB là :
18 x 1/3 = 6 ( cm )
- Vì tam giác MBC có chung chiều cao với hình thang ABCD nên ta có
chiều cao hình thang ABCD hay chiều cao tam giác MBC là:
42 x 2 : 6 = 14 ( cm )
- Độ dài đáy lớn CD là: 18 x 3/2 = 27 ( cm )
Suy ra ta có:
- Diện tích hình thang ABCD là:
( 27 + 18 ) x 14 : 2 = 315 ( cm2 )
Đáp số: 315 cm2
T
29 tháng 5 2023
Độ dài đoạn MB :
\(18\times\dfrac{1}{3}=6\left(cm\right)\)
Chiều cao \(\Delta MBC:\)
\(42\times2:6=14\left(cm\right)\)
Độ dài đáy CD :
\(18\times\dfrac{3}{2}=27\left(cm\right)\)
Diện tích hình thang ABCD:
\(\left(27+18\right)\times14:2=315\left(cm^2\right)\)
đ/s:.............
KN
9 tháng 2 2022
bài 2
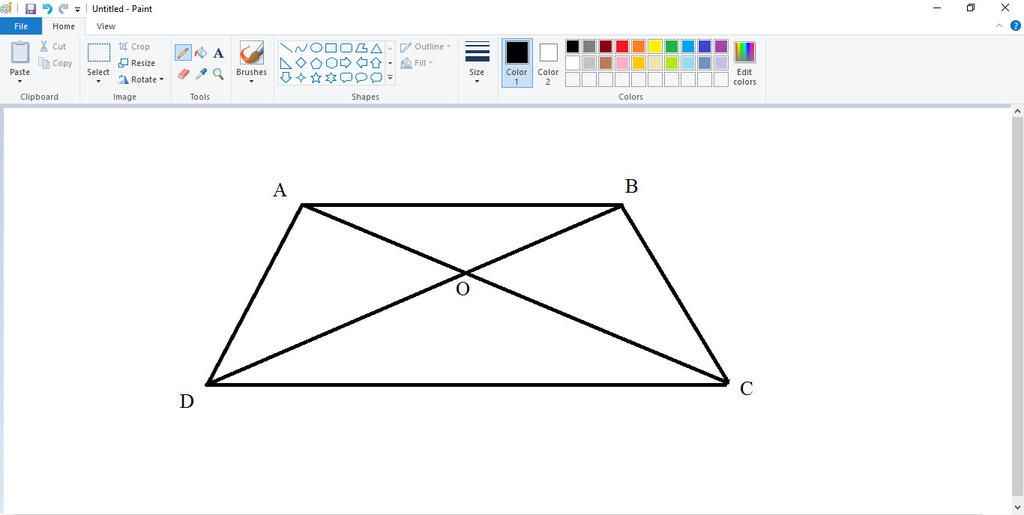
Cặp hình tam giác có diện tích bằng nhau là:
+ AOD và BOC
+ ADB và ABC
+ ADC và BCD
hình:
