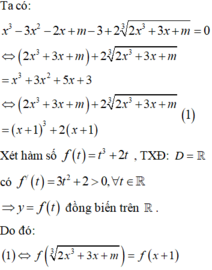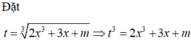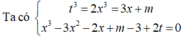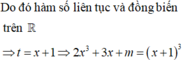làm thế nào để phân biệt đâu là ngiệm đâu là tập nghiệm của phương trình và bất phương trình ở phần kết luận ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án D
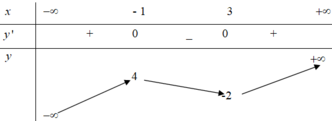
Số nghiệm của phương trình f ( x ) = m bằng
số giao điểm của đồ thị hàm số y = f ( x ) với
đường thẳng y = m
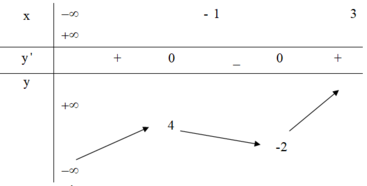
Từ bảng biến thiên suy ra phương trình có 3 nghiệm phân biệt khi − 2 < m < 4.

Đáp án D
Bất phương trình mx+ 6< 2x+3m . tương đương với ( m-2) x< 3( m-2)
Hay x< 3 ( với m< 2)
Vậy phần bù của tập nghiệm là ![]()

a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 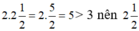 không là nghiệm của bất phương trình ,
không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 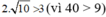 nên √10 không là nghiệm của bất phương trình,
nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: 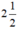 ; π; √10
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:


Đáp án là B
Đặt ![]()
![]()
Ta có
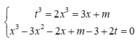
![]()
Xét hàm số
![]()
![]()
Do đó hàm số liên tục và đồng biến trên ℝ
![]()
![]()
Xét ![]()
![]()
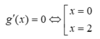
Bảng biến thiên

Từ bảng biến thiên suy ra -5 < -m < -1
![]()
Vậy tổng các phần tử của S bằng 9.

1.
\(\Leftrightarrow\left(m^2+4\right)x\ge2-m\)
Do \(m^2+4>0\) ; \(\forall m\)
\(\Rightarrow x\ge\dfrac{2-m}{m^2+4}\)
2.
\(\Leftrightarrow2mx-2x\ge m-1\Leftrightarrow2\left(m-1\right)x\ge m-1\)
- Với \(m>1\Rightarrow m-1>0\)
\(\Rightarrow x\ge\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\ge\dfrac{1}{2}\) \(\Rightarrow D=[\dfrac{1}{2};+\infty)\)
- Với \(m< 1\Rightarrow m-1< 0\Rightarrow x\le\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\le\dfrac{1}{2}\) \(\Rightarrow D=(-\infty;\dfrac{1}{2}]\)
- Với \(m=1\Leftrightarrow0\ge0\Rightarrow D=R\)
Quan sát 3 TH ta thấy không tồn tại m để tập nghiệm của BPT là \([1;+\infty)\)