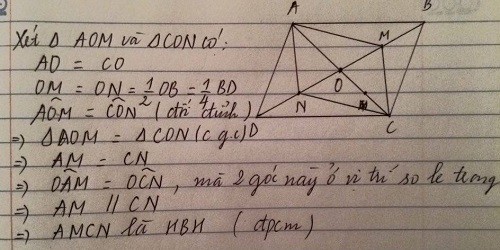
Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm của OB và OD.
a) Chứng minh tứ giác AMCN là hình bình hành bằng hai cách.
b) Tia AM cắt BC ở E, tia CN cắt AD ở F. Chứng minh ba đường thẳng AC, BD, EF đồng quy.

a: Ta có: ABCD là hình bình hành
nên AC và BD cắt nhau tại trung điểm của mỗi đường(1)
=>O là trung điểm chung của AC và BD
=>OB=OD
mà OM=1/2OB
và ON=1/2OD
nên OM=ON
hay O là trung điểm của MN
Xét tứ giác AMCN có
O là trung điểm của AC
O là trung điểm của MN
Do đó;AMCN là hình bình hành
b: Xét tứ giác AFCE có
AE//CF
AF//CE
Do đó: AFCE là hình bình hành
Suy ra: Hai đường chéo AC và FE cắt nhau tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,BD,EF đồng quy