Tìm x biết
a)x3=216
b)3x2=x2
c)x5=x4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 8 2017
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
HA
1
3 tháng 5 2022
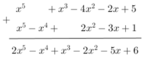
\(f\left(x\right)-g\left(x\right)=\left(x^5-3x^2+x^3-x^2-2x+5\right)-\left(x^2-3x+1+x^2-x^4+x^5\right)\)
\(f\left(x\right)-g\left(x\right)=x^5-3x^2+x^3-x^2-2x+5-x^2+3x-1-x^2+x^4-x^5\)
\(f\left(x\right)-g\left(x\right)=\left(x^5-x^5\right)+\left(-3x^2-x^2-x^2-x^2\right)+x^3+\left(-2x+3x\right)+\left(5-1\right)+x^4\)
\(f\left(x\right)-g\left(x\right)=-6x^2+x^3+x+4+x^4\)
\(f\left(x\right)-g\left(x\right)=x^4+x^3-6x^2+x+4\)
NN
2
9 tháng 4 2023
\(H\left(x\right)=F\left(x\right)+G\left(x\right)=\left(x^5-3x^2-x^3-x^2-2x+5\right)+\left(x^5-x^4+x^2-3x+x^2+1\right)\\ =x^5-3x^2-x^3-x^2-2x+5+x^5-x^4+x^2-3x+x^2+1\\ =\left(x^5+x^5\right)-x^4-x^3-\left(3x^2+x^2-x^2-x^2\right)-\left(2x+3x\right)+5\\ =2x^5-x^4-x^3-2x^2-5x+5\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
HP
26 tháng 12 2015
X1+X2=X3+X4=X5+X6=2
nên X1+X2+X3+X4+X5+X6=0
2+2+2=0
6=0(loại)
vậy không có giá trị nào thỏa mãn đề
1 tháng 4 2018
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
1 tháng 4 2018
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x): tự làm nha bạn
15 tháng 8 2021
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
\(a,x^3=216\)
=>\(x^3=6^3\)
=>x=6
Các câu sau như thế
\(x^3=216\Rightarrow x=\sqrt[3]{216}=6\)
\(3x^2=x^2\)
\(\Rightarrow3x^2-x^2=0\)
\(\Rightarrow x^2\left(3-1\right)=0\)
\(\Rightarrow x^2=0\Rightarrow x=0\)
\(x^5=x^4\)
\(\Rightarrow x^5-x^4=0\)
\(\Rightarrow x^4\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x^4=0\\x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)