Cho tam giác ABC và A'B'C', có trọng tâm lần lượt là G, G’ CMR: \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=3\overrightarrow{GG'}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.
b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.
c)
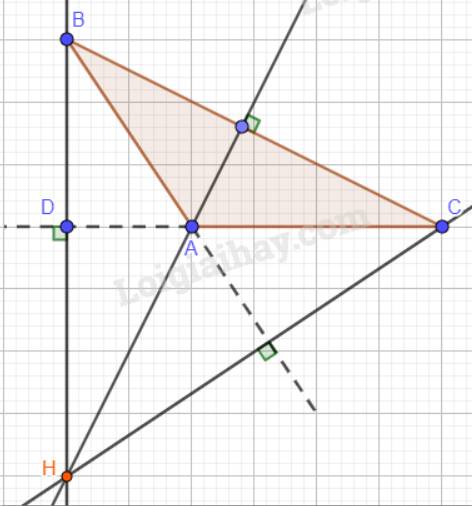
Nhận xét: H nằm ngoài tam giác ABC.

Lời giải:
Ta chứng minh bổ đề sau:
Với tam giác $ABC$ và $G$ là trọng tâm tam giác thì :
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Thật vậy. Gọi giao điểm \(AG\cap BC=T\Rightarrow T\) là trung điểm của tam giác. \(\Rightarrow \overrightarrow{BT}+\overrightarrow{CT}=0\)
Theo tính chất đường trung tuyến:
\(\overrightarrow{GA}=2\overrightarrow{TG}\Leftrightarrow \overrightarrow{GA}+2\overrightarrow{GT}=0\) \((1)\)
Mà \(\left\{\begin{matrix} \overrightarrow{GT}=\overrightarrow{GB}+\overrightarrow{BT}\\ \overrightarrow{GT}=\overrightarrow{GC}+\overrightarrow{CT}\end{matrix}\right.\Rightarrow 2\overrightarrow{GT}=\overrightarrow{GB}+\overrightarrow{GC}\) \((2)\)
Từ \((1),(2)\Rightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\)
Áp dụng CT trên vào bài toán thì: \(\left\{\begin{matrix} \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\\ \overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=0\end{matrix}\right.\)
Khi đó, từ \(\left\{\begin{matrix} \overrightarrow{GG'}=\overrightarrow{GA}+\overrightarrow{AA'}+\overrightarrow{A'G'}\\ \overrightarrow{GG'}=\overrightarrow{GB}+\overrightarrow{BB'}+\overrightarrow{B'G'}\\ \overrightarrow{GG'}=\overrightarrow{GC}+\overrightarrow{CC'}+\overrightarrow{C'G'}\end{matrix}\right.\)
\(\Rightarrow 3\overrightarrow{GG'}=\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\)
Ta có đpcm.