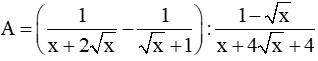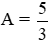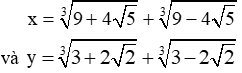Bài 3. Cho các điểm A(1;2) , B(0;1), C(-1;0), D(3;2) trong hệ trục tọa độ Oxy
a. Viết phương trình đường thẳng đi qua hai điểm A, B.
b. Chứng minh rằng tọa độ điểm C thỏa mãn phương trình AB. Từ đó suy ra A, B, C thẳng hàng.
c. Điểm D có thuộc đường thẳng AB hay không?
d. Viết phương trình đường thẳng đi qua điểm D và vuông góc với đường thẳng AB.
e. Tìm tọa độ giao điểm M, N của đường thẳng d với trục tung và trục hoành. Tính diện tích tam
giác OMN và đường cao OH của nó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy 1 điểm nối với 19 điểm còn lại ta được 19 đường thẳng
Làm như vậy với 20 điểm ta được 19 x 20 =380 đường thẳng
Nhưng trong 380 đường thẳng đó đã được tính 2 lần. Số đường thẳng thực tế là
380 : 2 =190 đường thẳng
Qua bài này ta có công thức tổng quát
Cho n điểm trong đó không có 3 điểm nào thẳng hàng . kẻ các đường thẳng đi qua các điểm đó
=> có \(\frac{n\times\left(n-1\right)}{2}\) đường thẳng
Hoc tốt .-.

Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)

Lời giải:
Vì $M\in (y=\frac{a}{x})$ nên:
$y_M=\frac{a}{x_M}\Rightarrow a=x_M.y_M=6.6=36$
Vậy hàm số có công thức $y=\frac{36}{x}(*)$
Giờ bạn thay tung độ (y) và hoành độ (x) của từng điểm vô xem có đúng với $(*)$ không thì thu được không có điểm nào thuộc ĐTHS.

 với x ³ 0 và x ¹ 1.
với x ³ 0 và x ¹ 1.

 với x > 2017
với x > 2017