Giải bài này giúp mk với mn ơi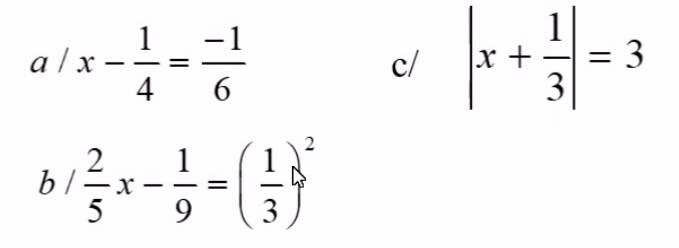
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{3}{7}+\left(-\dfrac{5}{2}\right)+\left(-\dfrac{3}{7}\right)=\dfrac{3}{7}-\dfrac{5}{2}-\dfrac{3}{7}=-\dfrac{5}{2}\)
b) \(B=\dfrac{4^2.2^3}{2^6}=\dfrac{\left(2^2\right)^2.2^3}{2^6}=\dfrac{2^4.2^3}{2^6}=\dfrac{2^7}{2^6}=2\)

giúp mk giải gấp 2 bài này với chiều tầm 3h mình qua lấy nha.cảm ơn mọi người nhiều ah.

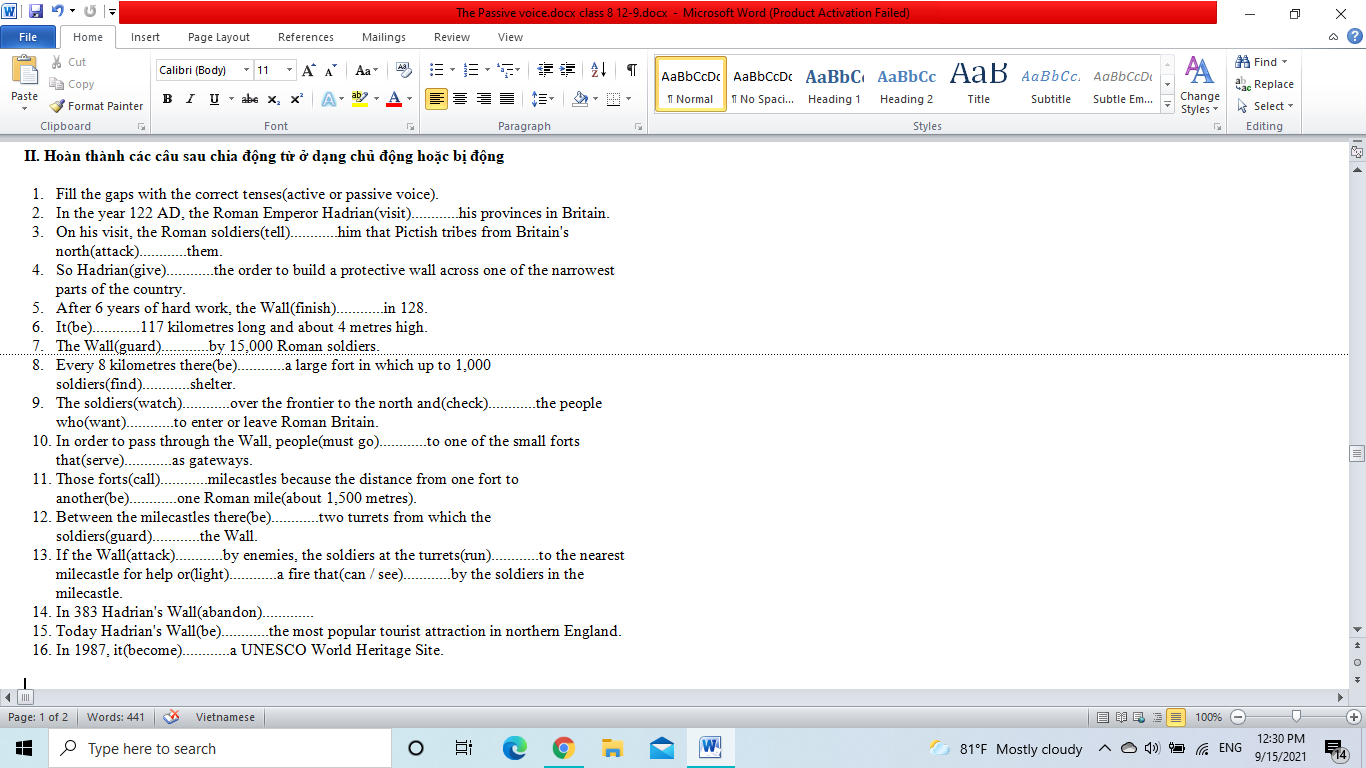
1 for - at
2 at - with
3 for - for
4 from - to
5 of - up
6 to - from
7 on - from - for
8 between - to - from


Bài 8:
a: Thay x=16 vào P, ta được:
\(P=\dfrac{4+2}{4-1}=\dfrac{6}{3}=2\)
b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:
\(P=\dfrac{\sqrt{2}+1+2}{\sqrt{2}+1-1}=\dfrac{3+\sqrt{2}}{\sqrt{2}}=3\sqrt{2}+2\)



Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)

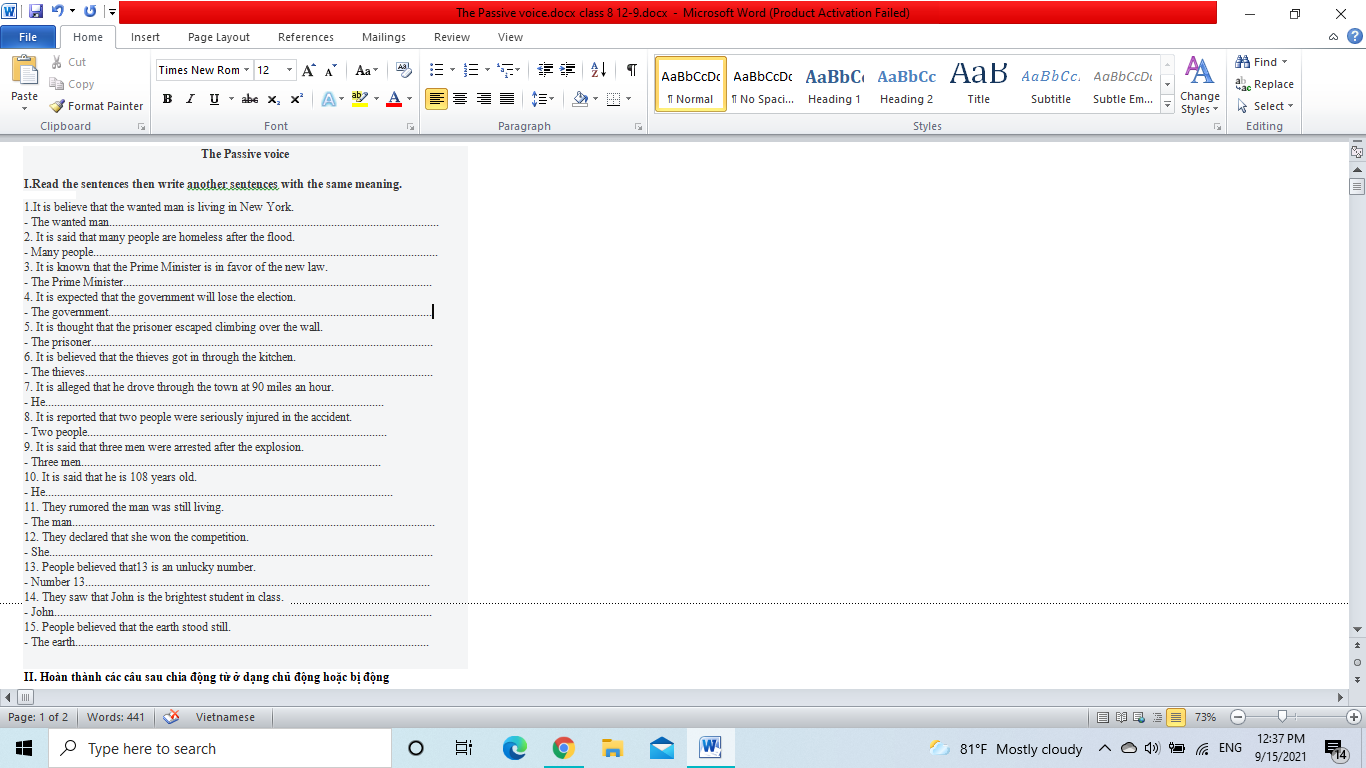 mn ơi giải giúp mk 2 bài này với chiều tầm 3h mình quay lại lấy bài nhé cảm ơn mn rất nhiều.
mn ơi giải giúp mk 2 bài này với chiều tầm 3h mình quay lại lấy bài nhé cảm ơn mn rất nhiều.






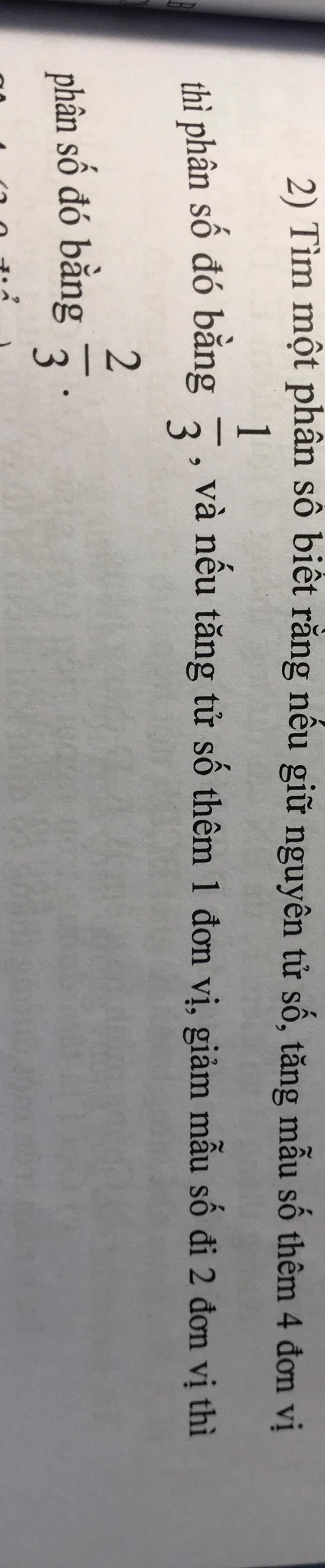
a) \(x-\dfrac{1}{4}=-\dfrac{1}{6}\Leftrightarrow x=-\dfrac{1}{6}+\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{12}\)
b) \(\dfrac{2}{5}x-\dfrac{1}{9}=\left(\dfrac{1}{3}\right)^2\Leftrightarrow\dfrac{2}{5}x=\dfrac{1}{9}+\dfrac{1}{9}\Leftrightarrow\dfrac{2}{5}x=\dfrac{2}{9}\Leftrightarrow x=\dfrac{5}{9}\)
c) \(\left|x+\dfrac{1}{3}\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=3\\x+\dfrac{1}{3}=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3-\dfrac{1}{3}\\x=-3-\dfrac{1}{3}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=-\dfrac{10}{3}\end{matrix}\right.\)
\(\left(a\right)\)
\(x-\dfrac{1}{4}=\dfrac{-1}{6}\)
\(x=\dfrac{1}{12}\)
/\(x+\dfrac{1}{3}\)/=3
=> \(x+\dfrac{1}{3}=3\) hoặc \(-x-\dfrac{1}{3}=3\)
=> x=\(\dfrac{8}{3}\) hoặc x= \(\dfrac{-10}{3}\)