cm: p=\(\dfrac{5^{125}-1}{5^{25}-1}\) là hợp số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
0
DT
1
13 tháng 9 2017
\(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3}{4}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}\)
\(=1\)
13 tháng 9 2017
\(\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}=\dfrac{1}{4}+\dfrac{3}{4}=1\)
LH
0
K
0
AT
30 tháng 6 2017
\(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{4\left(\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}\right)}+\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}{4\left(\dfrac{1}{5}-\dfrac{1}{25}-\dfrac{1}{125}-\dfrac{1}{625}\right)}\)
\(=\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{4}{4}=1\)
HN
5
VQ
26 tháng 6 2015
5^125 là số lẻ trừ 1 là số chẵn=>5^125-1 là hợp số(1)
5^25 là số lẻ trừ 1 là số chẵn=>5^25-1 là hợp số(2)
mà 5^125-1 và 5^25-1 lớn hơn 2 (3)
từ (1),(2) và (3)
=>5^125-1
____________
5^25-1 là hợp số
27 tháng 5 2022
a: \(=\left(1+\dfrac{4}{23}-\dfrac{4}{23}\right)+\left(\dfrac{5}{21}+\dfrac{16}{21}\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=2+\dfrac{1}{2}=\dfrac{5}{2}\)
b: \(=\left(\dfrac{1}{25}+\dfrac{5}{25}+\dfrac{25}{25}\right):\left(\dfrac{1}{25}-\dfrac{5}{25}-\dfrac{25}{25}\right)\)
\(=\dfrac{31}{25}:\dfrac{-29}{25}=\dfrac{-31}{29}\)
c: \(=\dfrac{\dfrac{1}{9}-\dfrac{1}{7}-\dfrac{1}{11}}{\dfrac{4}{9}-\dfrac{4}{7}-\dfrac{4}{11}}+\dfrac{\dfrac{3}{5}-\dfrac{3}{25}-\dfrac{3}{125}-\dfrac{3}{625}}{\dfrac{4}{5}-\dfrac{4}{25}-\dfrac{4}{125}-\dfrac{4}{625}}\)
=1/4+3/4
=1
GB
2
5 tháng 4 2023
\(\dfrac{5^{x+1}}{125}=\dfrac{1}{25^{x-2}}\\ \dfrac{5^{x+1}}{125}=\dfrac{1}{5^{2x-4}}\\ 5^{x+1}\cdot5^{2x-4}=125\\ 5^{x+1+2x-4}=5^3\\ 5^{\left(x+2x\right)+\left(1-4\right)}=5^3\\ 5^{3x-3}=5^3\\ 3x-3=3\\ 3x=6\\ x=2\)
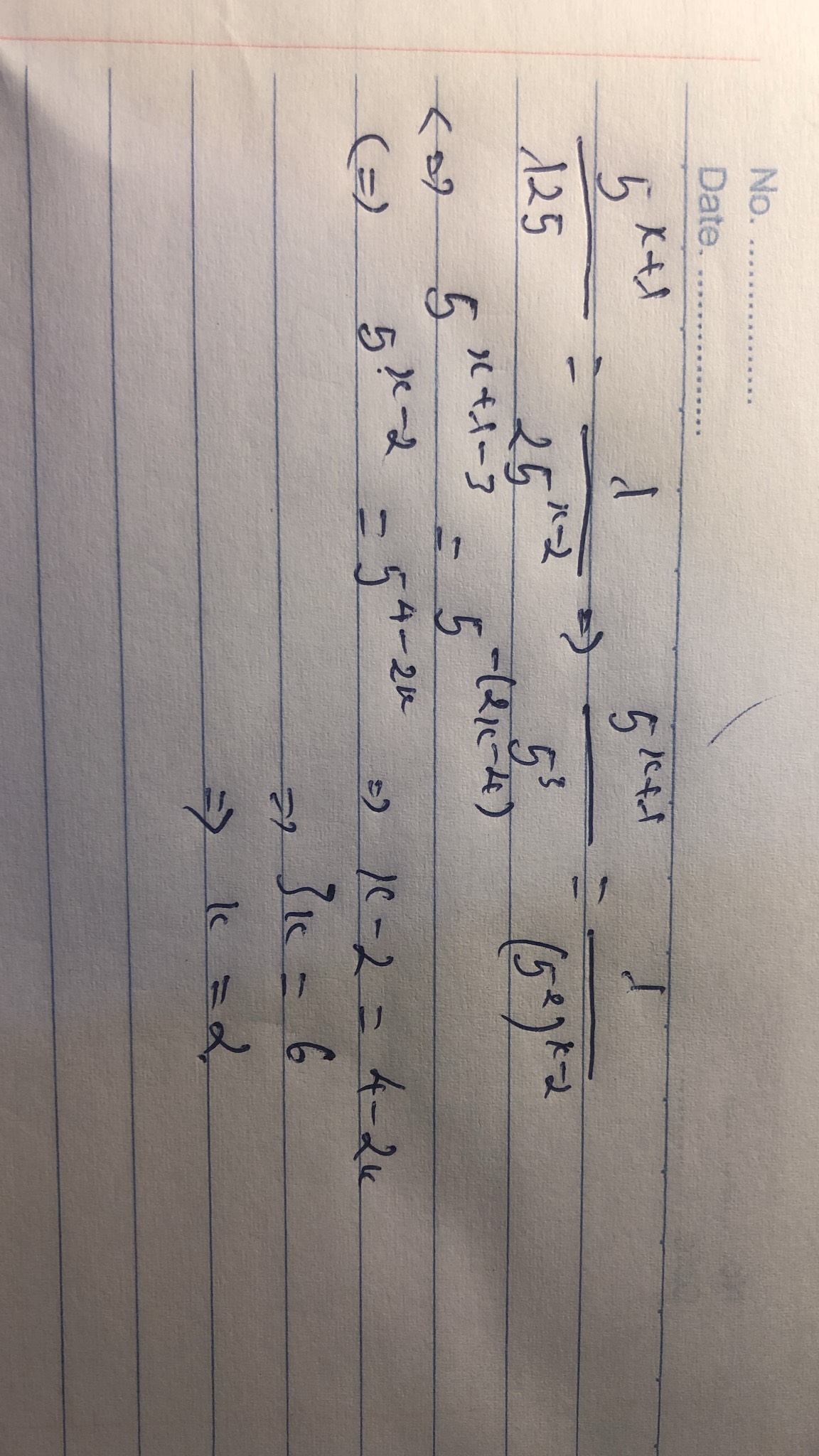
Lời giải:
Đặt \(5^{25}=a\). Khi đó:
\(p=\frac{5^{125}-1}{5^{25}-1}=\frac{(5^{25})^5-1}{5^{25}-1}=\frac{a^5-1}{a-1}=\frac{(a-1)(a^4+a^3+a^2+a+1)}{a-1}\)
\(=a^4+a^3+a^2+a+1\)
\(=(a^4+2a^2+1)+a^3+a-a^2\)
\(=(a^2+1)^2+a(a^2+1)-a^2\)
\(=(a^2+1)^2+6a(a^2+1)+9a^2-5a(a^2+1)-10a^2\)
\(=(a^2+1+3a)^2-5a(a^2+1+2a)\)
\(=(a^2+3a+1)^2-5a(a+1)^2=(a^2+3a+1)^2-5^{26}(a+1)^2\)
\(=[a^2+3a+1-5^{13}(a+1)][a^2+3a+1+5^{13}(a+1)]\)
Dễ thấy mỗi thừa số trên đều lớn hơn $2$, do đó $p$ là hợp số.