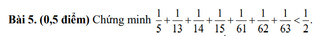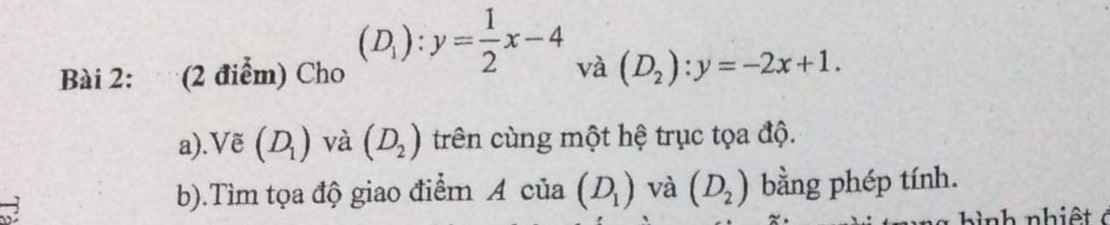Giúp mình bài 24 với mn ơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\left(x-3\right)^2-4=0\)
\(\Leftrightarrow\left(x-3-2\right)\left(x-3+2\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
2) \(x^2-2x=24\)
\(\Leftrightarrow x^2-2x-24=0\)
\(\Leftrightarrow x^2+4x-6x-24=0\)
\(\Leftrightarrow x\left(x+4\right)-6\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-4\end{matrix}\right.\)

\(f'\left(x\right)=x^2+2x\)
a.
\(f'\left(-3\right)=3\) ; \(f\left(-3\right)=-2\)
Phương trình tiếp tuyến:
\(y=3\left(x+3\right)-2\Leftrightarrow y=3x+7\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm, do hệ số góc tiếp tuyến bằng 3
\(\Rightarrow f'\left(x_0\right)=3\Rightarrow x_0^2+2x_0=3\Rightarrow x_0^2+2x_0-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=1\Rightarrow y_0=-\dfrac{2}{3}\\x_0=-3\Rightarrow y_0=-2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=3\left(x-1\right)-\dfrac{2}{3}=3x-\dfrac{11}{3}\\y=3\left(x+3\right)-2=3x+7\end{matrix}\right.\)
c. Tiếp tuyến song song (d) nên có hệ số góc bằng 8
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow x_0^2+2x_0=8\)
\(\Rightarrow\left[{}\begin{matrix}x_0=2\Rightarrow y_0=\dfrac{14}{3}\\x_0=-4\Rightarrow y_0=-\dfrac{22}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=8\left(x-2\right)+\dfrac{14}{3}=...\\y=8\left(x+4\right)-\dfrac{22}{3}=...\end{matrix}\right.\)

Em ơi bạn ấy có ghi ở cap là cần giúp bài 3 thôi mà.

Bài 2:
a: Xét ΔABC có
BI,CI là các đường phân giác
BI cắt CI tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
b: Ta có: \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
\(\widehat{DBI}=\widehat{IBC}\)(BI là phân giác của góc DBC)
Do đó: \(\widehat{DIB}=\widehat{DBI}\)
=>ΔDIB cân tại D
c: Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, EI//BC)
\(\widehat{ECI}=\widehat{ICB}\)(CI là phân giác của góc ECB)
Do đó: \(\widehat{EIC}=\widehat{ECI}\)
=>ΔEIC cân tại E
d: Ta có: ΔDIB cân tại D
=>DB=DI
Ta có: ΔEIC cân tại E
=>EI=EC
Ta có: DI+IE=DE
mà DI=DB
và EC=EI
nên DB+EC=DE
Bài 1:
a: Xét ΔABC có
BE,CF là các đường phân giác
BE cắt CF tại I
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
b: ta có: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}\)(BE là phân giác của góc ABC)
\(\widehat{ACF}=\widehat{FCB}=\dfrac{\widehat{ACB}}{2}\)(CF là phân giác của góc ACB)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABE}=\widehat{EBC}=\widehat{ACF}=\widehat{FCB}\)
c: ta có: \(\widehat{EBC}=\widehat{FCB}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
d: Xét ΔABE và ΔACF có
\(\widehat{ABE}=\widehat{ACF}\)
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
=>BE=CF
e:
Ta có: ΔAEB=ΔAFC
=>AE=AF
Ta có: AE+EC+AC
AF+FB=AB
mà AE=AF
và AC=AB
nên EC=FB
Xét ΔFIB và ΔEIC có
FB=EC
\(\widehat{FBI}=\widehat{ECI}\)
BI=CI
Do đó: ΔFIB=ΔEIC


Gọi số học sinh khối 6 là x
Theo đề, ta có: \(x-3\in BC\left(8;12;15\right)\)
\(\Leftrightarrow x-3\in\left\{120;240;360;...\right\}\)
\(\Leftrightarrow x\in\left\{123;243;363\right\}\)
mà 200<=x<=300
nên x=243
Gọi số học sinh khối 6 là a
a + 3 \(⋮8;12;15\)
\(\Rightarrow\) \(a+3\in BC\left(8;12;15\right)\)
8 = 2 . 3
12 = 22 . 3
15 = 3 . 5
\(\Rightarrow\) BCNN (8; 12; 15) = 22 . 3 . 5 = 60
Mà 203 < a + 3 < 303 học sinh
\(\Rightarrow\) a + 3 \(\in\) {240; 300}
\(\Rightarrow\) a \(\in\) {237; 207}