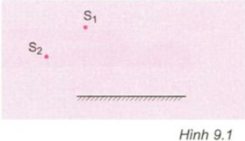
Cho hai điểm s1 và s2 đặt trước một gương phẳng như hình 37 hãy trình bày cách vẽ một tia sáng xuất phát từ S1 đến gương và cho tia phản xạ đi qua S2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


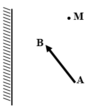
Vẽ ảnh N' của N qua gương
Nối M với N, MN cắt gương tại I
Nối I với N ta đc tia phản xạ của tia tới MI

a) Vẽ ảnh:
Vì ảnh và vật đối xứng nhau qua gương nên ta xác định ảnh của hai điểm sáng S1 và S2 bằng cách sau:
- Xác định ảnh S’1 của S1 bằng cách dựng S1H1 vuông góc với gương, trên tia đối của tia H1S1 lấy điểm S’1 sao cho S’1H1 = S1H1.S’1 là ảnh của S1 qua gương cần vẽ.
- Tương tự ta xác định được ảnh S’2 của S2 qua gương.
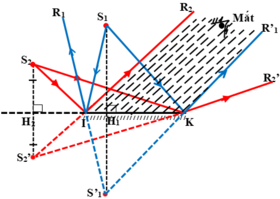
b) Từ S1, S2 ta vẽ hai chùm tia sáng sao cho hai tia ngoài cùng đến hai mép IK của gương, khi đó hai tia tới từ S1 và S2 cho chùm tia phản xạ có đường kéo dài đi qua ảnh của chúng.
c) Để mắt quan sát được cả hai ảnh S’1 và S’2 của hai điểm sáng trong gương thì mắt phải đặt tại vùng giao nhau của vùng nhìn thấy ảnh S’1 (là vùng R1IKR’1) và vùng nhìn thấy ảnh S’2 (là vùng R2IKR’2). Hai vùng này giao nhau tạo thành vùng R2IKR’1 (là vùng gạch chéo), mắt đặt tại vùng này sẽ nhìn thấy đồng thời hai ảnh của hai điểm sáng.


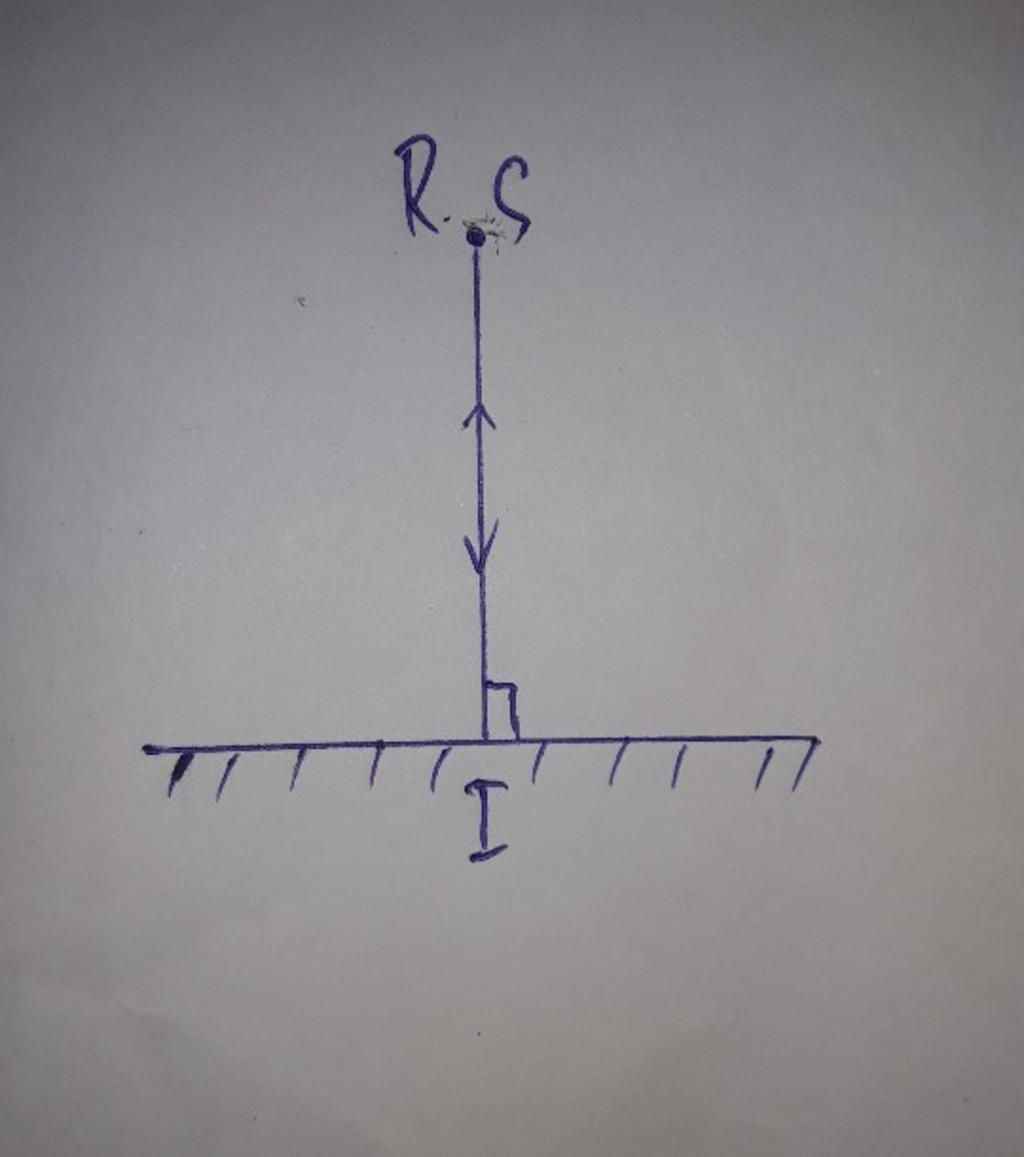
a) vẽ hình như trên.
b) chứng minh hai tia JR // SI
Ta có do hai pháp tuyển N1 và N2 vuông góc nên ta có \(i'+i_1 = 90^0\)
mà \(i=i'; i_1 = i_1' => i+i'+i_1+i_1' = 90+90 = 180^0\)
=> JR//SI (tổng hai góc trong cùng phía bằng 180 độ)

Cách vẽ:
Gọi: S' là ảnh của S qua gương 1.
\(\Rightarrow\) Tia tới qua gương 1 tạo ra tia phản xạ đi qua S'.
Gọi: S'' là ảnh của S qua gương 2.
\(\Rightarrow\) Tia tới khi qua gương 2 cho tia phản tạo ta tia phản xạ đi qua S
\(\Rightarrow\) Tia tới sẽ đi qua S''.
Giả sử S', S'' cắt G tại A và G' tại B.
\(\Rightarrow\) SABS là đường truyền tia sáng cần vẽ.
Chứng minh:
Ta có: \(\left\{{}\begin{matrix}\widehat{SAG}=\widehat{OAB}\\\widehat{OBA}=\widehat{SBG'}\end{matrix}\right.\)
\(\widehat{ASB}+\widehat{SAB}+\widehat{SBA}=90^0\)
\(\widehat{SAB}+2\widehat{OAB}=180^0\) \(\Rightarrow\widehat{SAB}=180^0-2\widehat{0AB}\)
\(\widehat{SBA}+2\widehat{OAB}=180^0\Rightarrow\widehat{SBA}=180^0-2\widehat{OAB}\)
\(\Rightarrow\widehat{ASB}+180^0-2\widehat{0AB}+180^0-2\widehat{OBA}=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\left(180^0-\widehat{0AB}-\widehat{0BA}\right)=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\alpha=180^0\)
\(\Rightarrow\widehat{ASB}=180^0-2\alpha\)
Vậy \(\widehat{ASB}\) không phụ thuộc vào góc tới mà phụ thuộc vào góc hợp bởi 2 gương (đpcm).