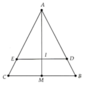
Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm E, AB lấy điểm D sao cho AD=EC. Trung điểm I của DE chuyển động trên đường nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tương tự 2A.
Cho D º B, E º C Þ Vị trí điểm I.
CHo D º A, E º A Þ Vị trí điểm I.
Kết luận: I thuộc trung trực của BC.

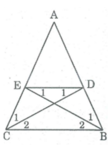
Ta có: BD = DE ⇒ ∆ BDE cân tại D
∠ B 1 = ∠ E 1
Mà ∠ E 1 = ∠ B 2 (so le trong)
⇒ ∠ B 1 = ∠ B 2
DE = EC ⇒ ∆ DEC cân tại E
⇒ ∠ D 1 = ∠ C 1
∠ D 1 = ∠ C 2 (so le trong)
⇒ ∠ C 1 = ∠ C 2
Vậy khi BE là tia phân giác của ∠ (ABC) , CD là tia phân giác của ∠ (ACB) thì BD = DE = EC

Tam giác BDE.m là trung điểm của DE,N là trung điểm của BE => MN là đường trung bình của tam giác BDE=> MN//DB <=> MN//BA
tương tự c/m MQ là đường trung điểm của tam giác DEC => MQ//EC hay MQ//AC.Mà AC vuông góc AB=> MN vuông góc PQ => góc MNQ = 90
Tượng từ theo cách đường trung bình thì các góc còn lại của tứ giác MNPQ = 90 => là hình chữ nhạt
MN là đường trung bình => MN = 1/2 DB,MQ=1/2 EC mà EC=DB => MN=DB
=> tam giác là hình vuông (DHNB)

a: Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Do đó: DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BDEC là hình thang cân