Cho a,b là các số nguyên dương thỏa mãn: log2(log2a(log2b21000)) = 0. Tính giá trị lớn nhất của ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
28 tháng 5 2018
Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
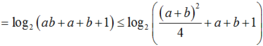
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
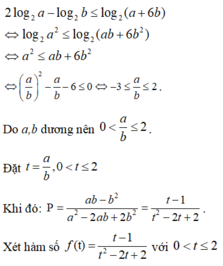
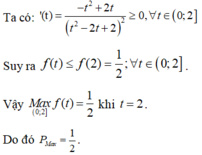
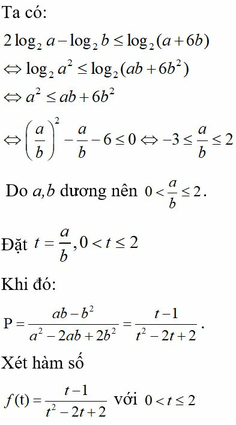
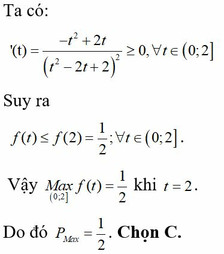


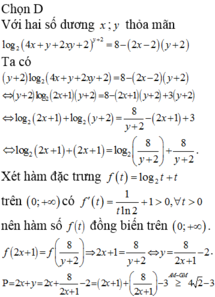
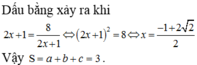

\(\Rightarrow log_{2^a}\left(log_{2^b}2^{1000}\right)=1\)
\(\Rightarrow log_{2^b}2^{1000}=2^a\)
\(\Rightarrow\dfrac{1000}{b}=2^a\)
\(\Rightarrow\dfrac{1000}{2^a}=b\)
\(\Rightarrow\dfrac{2^3.125}{2^a}=b\)
Do a;b nguyên dương \(\Rightarrow2^3⋮2^a\Rightarrow a=\left\{1;2;3\right\}\)
Giờ thì tìm b tương ứng a rồi tính 3 giá trị a.b, so sánh => đáp án