Question

[Phạm Đức Minh]

Chứng minh n⁴+2n³-n²-2n chia hết cho 24 với mọi n

Answer 1

[Akai Haruma]

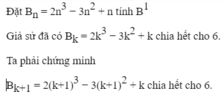
Lời giải:

Đặt \(A=n^4+2n^3-n^2-2n\)

\(\Leftrightarrow A=(n+2)(n^3-n)=n(n+2)(n^2-1)\)

Ta cm \(A\vdots 3\)

+) Nếu \(n\equiv 0\pmod 3\Rightarrow A\vdots 3\)

+) Nếu \(n\equiv \pm 1\pmod 3\Rightarrow n^2\equiv 1\pmod 3\Leftrightarrow n^2-1\vdots 3\)

\(\Rightarrow A\vdots 3\)

Từ hai TH trên suy ra \(A\vdots 3(1)\)

Ta cm \(A\vdots 8\)

\(A=n(n+2)(n-1)(n+1)\)

+) Nếu \(n\equiv 0\pmod 4\Rightarrow\left\{\begin{matrix} n+2\equiv 0\pmod 2\\ n\equiv 0\pmod 4\end{matrix}\right.\Rightarrow n(n+2)\vdots 8\Rightarrow A\vdots 8\)

+) Nếu \(n\equiv 1\pmod {4}\Rightarrow \left\{\begin{matrix} n-1\equiv 0\pmod 4\\ n+1\equiv 0\pmod 2\end{matrix}\right.\Rightarrow (n-1)(n+1)\vdots 8\Rightarrow A\vdots 8\)

+) Nếu \(n\equiv 2\pmod 4\Rightarrow\left\{\begin{matrix} n\equiv 0\pmod 2\\ n+2\equiv 2+2\equiv 0\pmod 4\end{matrix}\right.\Rightarrow n(n+2)\vdots 8\Rightarrow A\vdots 8\)

+) Nếu \(n\equiv 3\pmod 4\Rightarrow\left\{\begin{matrix} n-1\equiv 0\pmod 2\\ n+1\equiv 3+1\equiv 0\pmod 4\end{matrix}\right.\Rightarrow (n-1)(n+1)\vdots 8\Rightarrow A\vdots 8\)

Từ các TH trên suy ra \(A\vdots 8(2)\)

Từ \((1),(2),\text{UCLN(8,3)=1}\Rightarrow A\vdots 24\)

Answer 2

[Đời về cơ bản là buồn... cười!!!]

Ta có: \(n^4+2n^3-n^2-2n\)

\(=\left(n^4+2n^3\right)-\left(n^2+2n\right)\)

\(=n^3\left(n+2\right)-n\left(n+2\right)\)

\(=\left(n+2\right)\left(n^3-n\right)\)

=> \(n^4+2n^3-n^2-2n⋮24\)