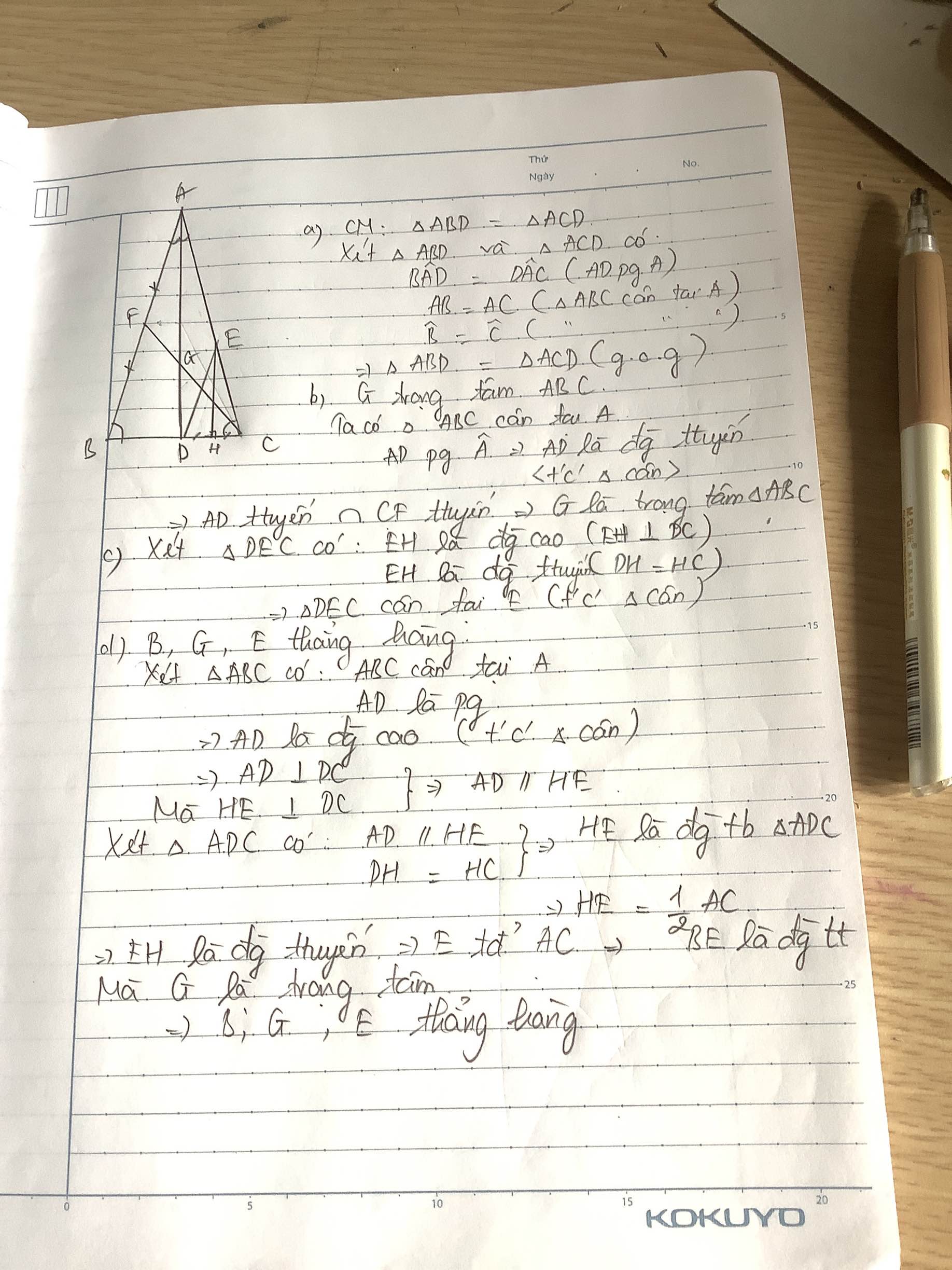cho tam giác ABC có G là trọng tâm. Đường thẳn d không cắt các cạnh của tam giác ABC. Gọi A',B',C',G' lần luotej là hình chiếu của A,B,C,G trên đường thẳng d. Chứng minh GG' = (AA' + BB' + CC') : 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Gọi E là trung điểm AG và AD là trung tuyến
Mà G là trọng tâm nên \(AE=EG=GD=\dfrac{1}{3}AD\)
Gọi E' và D' lần lượt là hình chiếu của E và D lên d
Ta có AA'//BB'//CC'//DD'//EE'//GG' (cùng vuông góc với d)
Xét hình thang AA'G'G có E là trung điểm AG và EE'//AA'//GG' nên E' là trung điểm A'G'
Do đó EE' là đtb hình thang AA'G'G
Do đó \(EE'=\dfrac{AA'+GG'}{2}\left(1\right)\)
Xét hình thang BB'C'C có D là trung điểm BC và DD'//BB'//CC' nên D' là trung điểm B'C'
Do đó DD' là đtb hình thang BB'C'C
Do đó \(DD'=\dfrac{BB'+CC'}{2}\left(2\right)\)
Xét hình thang EE'D'D có G là trung điểm ED và EE'//DD'//GG' nên G' là trung điểm E'D'
Do đó GG' là đtb hình thang EE'D'D
Do đó \(2GG'=EE'+DD'\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow2GG'=\dfrac{AA'+GG'+BB'+CC'}{2}\)
\(\Rightarrow4GG'=AA'+BB'+GG'+CC'\\ \Rightarrow3GG'=AA'+BB'+CC'\\ \Rightarrow GG'=\dfrac{AA'+BB'+CC'}{3}\)
E sửa lại cái đề đi nha
Kẻ MN đối ME sao cho \(MN=ME\); DE cắt AB tại F
Mà \(AM=MD;\widehat{AMN}=\widehat{EMD}\left(đối.đỉnh\right)\)
Do đó \(\Delta AMN=\Delta DME\left(c.g.c\right)\)
\(\Rightarrow\widehat{ANM}=\widehat{MED};AN=DE\)
Mà 2 góc này ở vị trí so le trong nên AN//DE
Vì tg ABC đều nên \(\widehat{FAD}=60^0;\widehat{ACB}=60^0\)
Mà tg AFD vuông tại F nên \(\widehat{ADF}=90^0-\widehat{FAD}=30^0\)
Do đó \(\widehat{ADF}=\widehat{EDC}=30^0\left(đối.đỉnh\right)\)
Ta có \(\widehat{ECD}=\widehat{ECB}-\widehat{ACB}=90^0-60^0=30^0\Rightarrow\widehat{ECD}=\widehat{EDC}\)
Do đó tg EDC cân tại E nên \(ED=EC\)
\(\Rightarrow EC=AN\)
Ta có AN//DE;DE⊥AB nên AN⊥AB
Vì \(\left\{{}\begin{matrix}\widehat{NAB}=\widehat{ECB}=90^0\\AN=EC\\AB=AC\end{matrix}\right.\) nên \(\Delta ANB=\Delta CEB\left(2.cgv\right)\)
\(\Rightarrow AB=AE\left(1\right);\widehat{NBA}=\widehat{EBC}\\ \Rightarrow\widehat{NBA}+\widehat{ABE}=\widehat{EBC}+\widehat{ABE}=\widehat{ABC}=60^0\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\Delta BNE\) đều
Mà BM là trung tuyến \(\left(NM=ME\right)\) nên cũng là p/g
Vậy \(\widehat{MBE}=\dfrac{1}{2}\widehat{NBE}=30^0\)

a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
b) Ta có: ΔABD=ΔACD(cmt)
nên DB=DC(hai cạnh tương ứng)
mà B,D,C thẳng hàng(gt)
nên D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)

a: XétΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
DO đó: ΔABD=ΔACD
b: XétΔABC có
AD là đường trung tuyến
CF là đường trung tuyến
AD cắt CF tại G
Do đó: G là trọng tâm của ΔABC