Vẽ hình nữa nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2023
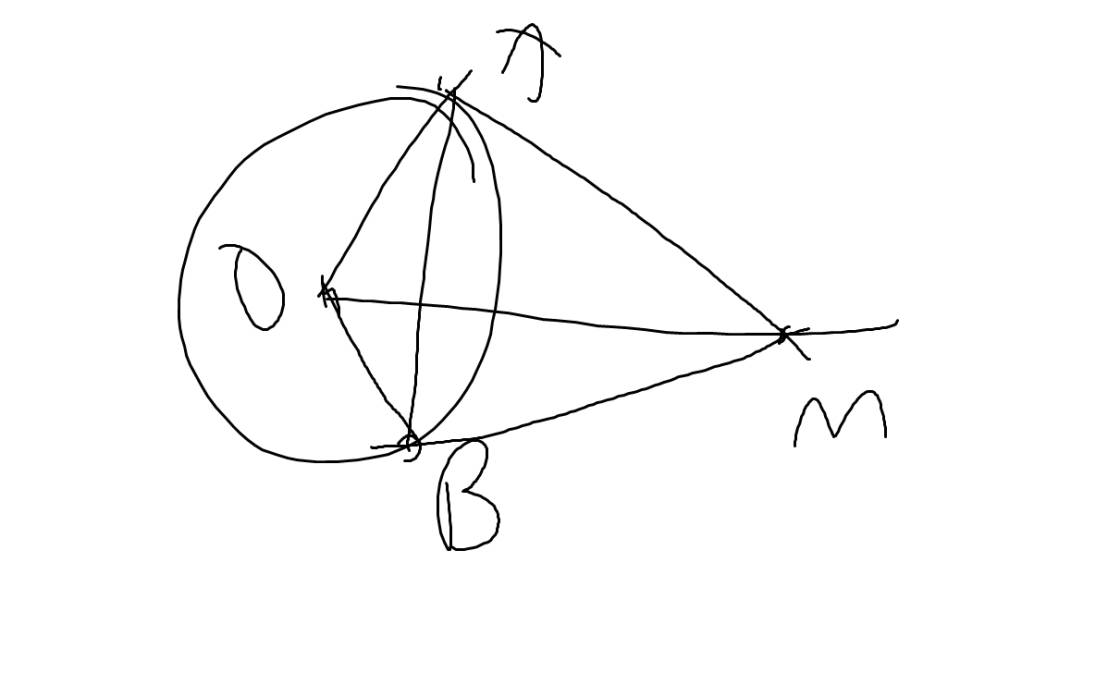
Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
17 tháng 12 2023
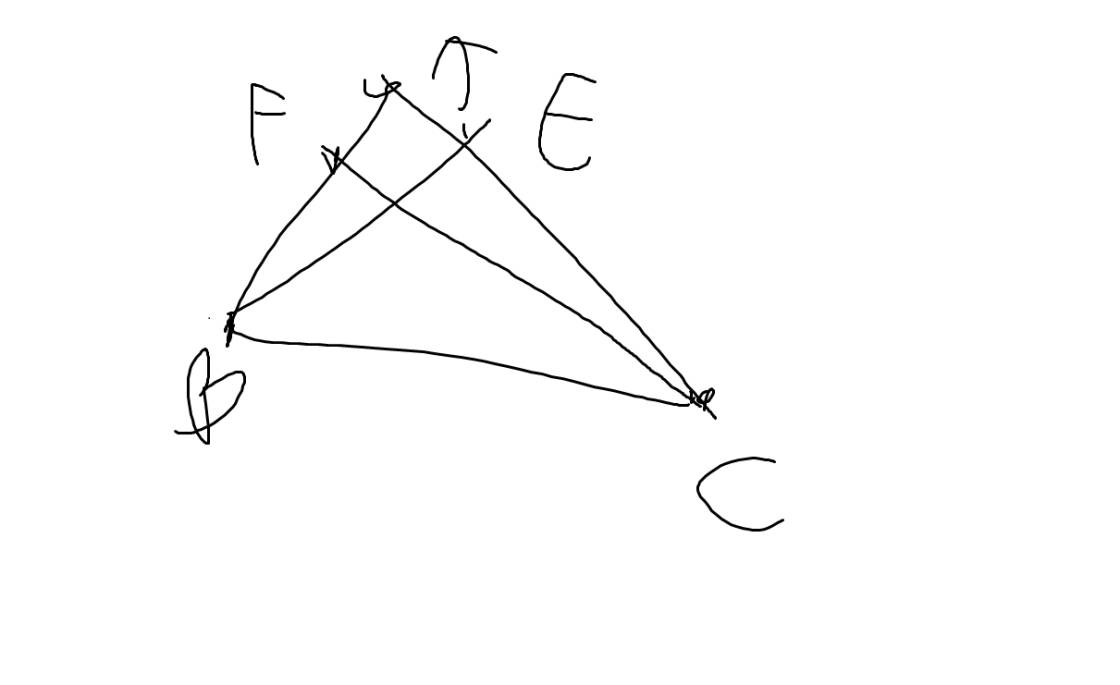
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
TD
0
AH
Akai Haruma
Giáo viên
21 tháng 12 2022
Lời giải:
Vì $B,D$ đối xứng với nhau qua $AC$ nên $AC$ chính là trung trực của $BD$
$\Rightarrow AB=AD; CB=CD$. Mà $ABC$ là tam giác cân tại $B$ nên $AB=BC$
$\Rightarrow AB=BC=AD=CD$
Xét tam giác $ABD$ và $CBD$ có:
$AB=CB$ (cmt)
$BD$ chung
$AD=CD$ (cmt)
$\Rightarrow \triangle ABD=\triangle CBD$ (c.c.c)
NN
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
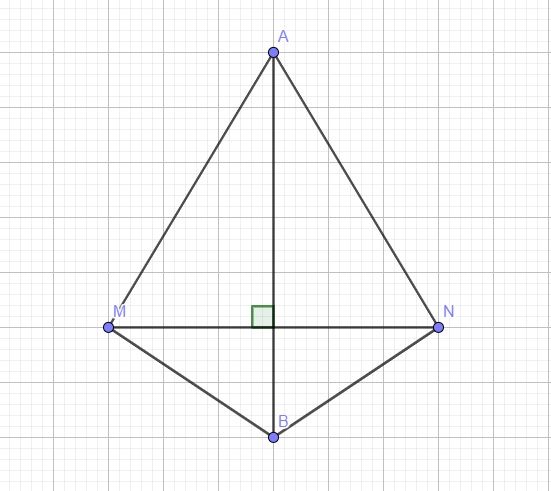
Do A thuộc trung trực đoạn MN nên \(AM=AN\)
Do B thuộc trung trực đoạn MN nên \(BM=BN\)
Xét 2 tam giác MAB và NAB có:
\(\left\{{}\begin{matrix}AM=AN\left(cmt\right)\\BM=BN\left(cmt\right)\\AB\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta MAB=\Delta NAB\left(c.c.c\right)\)
a: Xét (O) có
\(\widehat{EBF}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{EBF}=90^0\)
Xét (O) có
\(\widehat{EAF}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{EAF}=90^0\)
Xét ΔDEF có
EB là đường cao ứng với cạnh FD
FA là đường cao ứng với cạnh DE
EB cắt FA tại H
Do đó: H là trực tâm của ΔDEF
b: Xét tứ giác DAHB có
\(\widehat{DAH}+\widehat{DBH}=180^0\)
nên DAHB là tứ giác nội tiếp
hay D,A,H,B cùng thuộc 1 đường tròn
c: Ta có: I là tâm của đường tròn ngoại tiếp tứ giác DAHB
Suy ra: IA=IB
hay I nằm trên đường trung trực của AB(1)
Ta có: O là tâm đường tròn ngoại tiếp tứ giác ABFE
Suy ra: OA=OB
hay O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OI là đường trung trực của AB
hay OI\(\perp\)AB
d: Điểm K ở đâu vậy bạn?