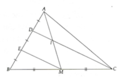
Cho tam giác ABC . Lấy D,E trên cạnh AB sao cho AD=DE=EB . Gọi M là trung điểm của BC , CD và AM cắt nhau tại I
c/m AI=IM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2017
Hình thì tự vẽ nha :))
Nối EM lại .
Có EM là đường trung bình của \(\Delta ABC\)
=> EM // DC
Lại có : DI cắt AE tại trung điểm D
và : EM // DI (EM // DC)
=> DI là đường trung bình của \(\Delta AEM\)
=> DI cắt AM tại trung điểm I
=> IA = IM
13 tháng 10 2021
Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DB
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DC
Xét ΔAME có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay AI=IM
21 tháng 10 2021
Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DK
Xét ΔAEM có
D là trung điểm của AE
DK//EM
Do đó: K là trung điểm của AM
hay KA=KM
27 tháng 7 2021
a) Xét ΔBCD có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//CD và \(ME=\dfrac{CD}{2}\)(Định lí 2 về đường trung bình của tam giác)
b) Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
c) Xét ΔAEM có
D là trung điểm của AE
I là trung điểm của AM
Do đó: DI là đường trung bình của ΔAEM
Suy ra: DI//EM và \(DI=\dfrac{EM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: \(DI=\dfrac{EM}{2}\)(cmt)
nên \(EM=2\cdot DI\)
\(\Leftrightarrow\dfrac{DC}{2}=2\cdot DI\)
\(\Leftrightarrow DC=4\cdot DI\)
\(\Leftrightarrow DC-DI=4DI-DI\)
\(\Leftrightarrow CI=3DI\)
CM
24 tháng 10 2017
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
26 tháng 1 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
b: Xét ΔADH và ΔAEH có
AD=AE
góc DAH=góc EAH
AH chung
=>ΔADH=ΔAEH
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Xét tam giác BDC có E là trung điểm của BD. M là trung điểm của BC=> ME//DC( Tính chất đường trung bình) mà I thuộc DC nên ME//DI
Xét tam giác AEM có D là trung điểm của AE( AD=DE), DI//EM=> I là trung điểm của AM( tính chất đường trung bình)=> AI=IM( đpcm)
Bạn tự vẽ hình nha!!!
cam on nhieu