(x+2)(x+3)(x+4)(x+5)-24
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5 x 6 = 30 2 x 6 = 12 3 x 6 = 18 4 x 6 = 24
6 x 5 = 30 6 x 2 = 12 6 x 3 = 18 6 x 4 = 24

1) 2(x + 5) + 3(x + 7) = 41
2x + 10 + 3x + 21 = 41
5x + 31 = 41
5x = 10
x = 2
6) 7(x - 1) + 5(3 - x) = 11x - 10
7x - 7 + 15 - 5x = 11x - 10
2x + 8 = 11x - 10
-9x = -18
x = 2
2) 5(x + 6) + 2(x - 3) = 38
5x + 30 + 2x - 6 = 38
7x + 24 = 38
7x = 14
x = 2
7) 4(2 + x) + 3(x - 2) = 12
8 + 4x + 3x - 6 = 12
7x + 2 = 12
7x = 10
x = 10/7
3) 7(5 + x) + 2(x - 10) = 15
35 + 7x + 2x - 20 = 15
9x + 15 = 15
9x = 0
x = 0
8) 5(2 + x) + 4(3 - x) = 10x - 15
10 + 5x + 12 - 4x = 10x - 15
x + 22 = 10x - 15
9x = 37
x = 37/9
4) 3(x + 4) + (8 - 2x) = 22
3x + 12 + 8 - 2x = 22
x + 20 = 22
x = 2
9) 7(x - 2) + 5(3 - x) = 11x - 6
7x - 14 + 15 - 5x = 11x - 6
2x + 1 = 11x - 6
-9x = -7
x = 7/9
5) 4(x + 5) + 3(7 - x) = 49
4x + 20 + 21 - 3x = 49
x + 41 = 49
x = 8
10) 5(3 - x) + 5(x + 4) = 6 + 4x
15 - 5x + 5x + 20 = 6 + 4x
35 = 6 + 4x
4x = 29
x = 29/4

Bài làm:
a) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt \(x^2+5x+5=t\)\(\Rightarrow\left(t-1\right)\left(t+1\right)+1=t^2-1+1=t^2\)
\(=\left(x^2+5x+5\right)^2\)
b) Tương tự như a phân tích và đặt ra được: \(t^2-1-24=t^2-25=\left(t-5\right)\left(t+5\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)=x\left(x+5\right)\left(x^2+5x+10\right)\)
c) \(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15\)
\(=\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+15\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15\)
Đặt \(x^2+8x+11=t\)\(\Rightarrow\left(t-4\right)\left(t+4\right)+15=t^2-16+15=t^2-1\)
\(=\left(t-1\right)\left(t+1\right)=\left(x^2+8x+10\right)\left(x^2+8x+12\right)\)
\(=\left(x^2+8x+10\right)\left(x+2\right)\left(x+6\right)\)
d) \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left[\left(x+2\right)\left(x+5\right)\right]\left[\left(x+3\right)\left(x+4\right)\right]-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(x^2+7x+11=t\)\(\Rightarrow\left(t-1\right)\left(t+1\right)-24=t^2-1-24=t^2-25\)
\(=\left(t-5\right)\left(t+5\right)=\left(x^2+7x+6\right)\left(x^2+7x+16\right)\)
\(=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)
Làm mẫu cho 1 vd:
a, (x+1)(x+2)(x+3)(x+4)+1
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)(1)
Đặt \(y=x^2+5x+5\)
Khi đó ::
(1) = \(\left(y-1\right)\left(y+1\right)+1\)
\(=y^2-1+1=y^2\)
Thay vào ta được: \(\left(x^2+5x+5\right)^2\)

1) Ta có: \(\left(x+2\right)^2+\left(x-3\right)^2\)
\(=x^2+4x+4+x^2-6x+9\)
\(=2x^2-2x+13\)
2) Ta có: \(\left(4-x\right)^2-\left(x-3\right)^2\)
\(=\left(4-x-x+3\right)\left(4-x+x-3\right)\)
\(=-2x+7\)
3) Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)^2\)
\(=x^2-25-x^2-10x-25\)
=-10x-50
4) Ta có: \(\left(x-3\right)^2-\left(x-4\right)\left(x+4\right)\)
\(=x^2-6x+9-x^2+16\)
=-6x+25
5) Ta có: \(\left(y^2-6y+9\right)-\left(y-3\right)^2\)
\(=y^2-6y+9-y^2+6y-9\)
=0
6) Ta có: \(\left(2x+3\right)^2-\left(2x-3\right)\left(2x+3\right)\)
\(=4x^2+12x+9-4x^2+9\)
=12x+18

nhiều quá :((
\(a,2\left(x-5\right)-3\left(x+7\right)=14\)
\(2x-10-3x-21=14\)
\(-x-31=14\)
\(-x=45\)
\(x=45\)
\(b,5\left(x-6\right)-2\left(x+3\right)=12\)
\(5x-30-2x-6=12\)
\(3x-36==12\)
\(3x=48\)
\(x=16\)
\(c,3\left(x-4\right)-\left(8-x\right)=12\)
\(3x-12-8+x=0\)
\(4x-20=0\)
\(4x=20\)
\(x=5\)
Cố nốt nha bn !
cảm ơn, bn nha:)))
mà hình như bạn TOP 3 trả lời câu hỏi pải ko nhỉ???

\(a)x=\dfrac{1}{4}+\dfrac{5}{13}=\dfrac{33}{52}.\\ b)\dfrac{x}{3}=\dfrac{2}{3}+\dfrac{-1}{7}.\\ \Leftrightarrow\dfrac{x}{3}=\dfrac{11}{21}.\\ \Leftrightarrow\dfrac{7x}{21}=\dfrac{11}{21}.\\ \Rightarrow7x=11.\\ \Leftrightarrow x=\dfrac{11}{7}.\\ c)\dfrac{x}{3}=\dfrac{16}{24}+\dfrac{24}{36}=\dfrac{2}{3}+\dfrac{2}{3}=\dfrac{4}{3}.\\ \Rightarrow x=4.\\ d)\dfrac{x}{15}=\dfrac{1}{5}+\dfrac{2}{3}=\dfrac{13}{15}.\\ \Rightarrow x=13.\)

a)\(\dfrac{x}{60}=-\dfrac{3}{4}\)
\(\Rightarrow x\cdot4=60\cdot\left(-3\right)\)
\(x\cdot4=-180\)
x=45
b)\(\dfrac{2}{5}=\dfrac{12}{x}\)
\(\Rightarrow2x=5\cdot12\)
\(2x=60\)
x=30
c)\(x-\dfrac{5}{7}=\dfrac{6}{21}\)
\(x=\dfrac{2}{7}+\dfrac{5}{7}\)
x=1
d)\(x+\dfrac{7}{8}=\dfrac{63}{24}\)
\(x=\dfrac{21}{8}-\dfrac{7}{8}\)
\(\dfrac{14}{8}\)
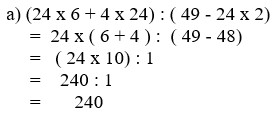

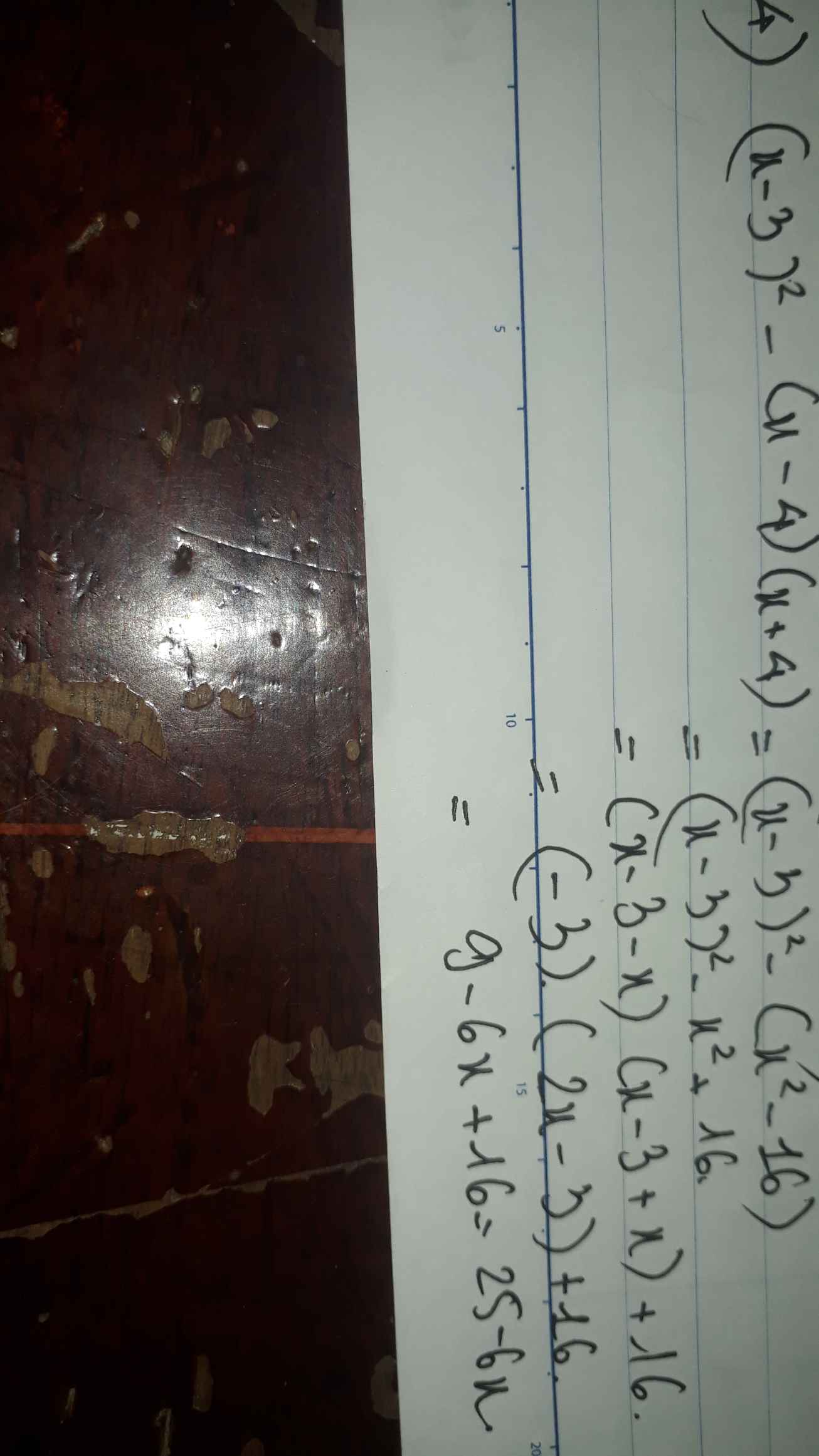
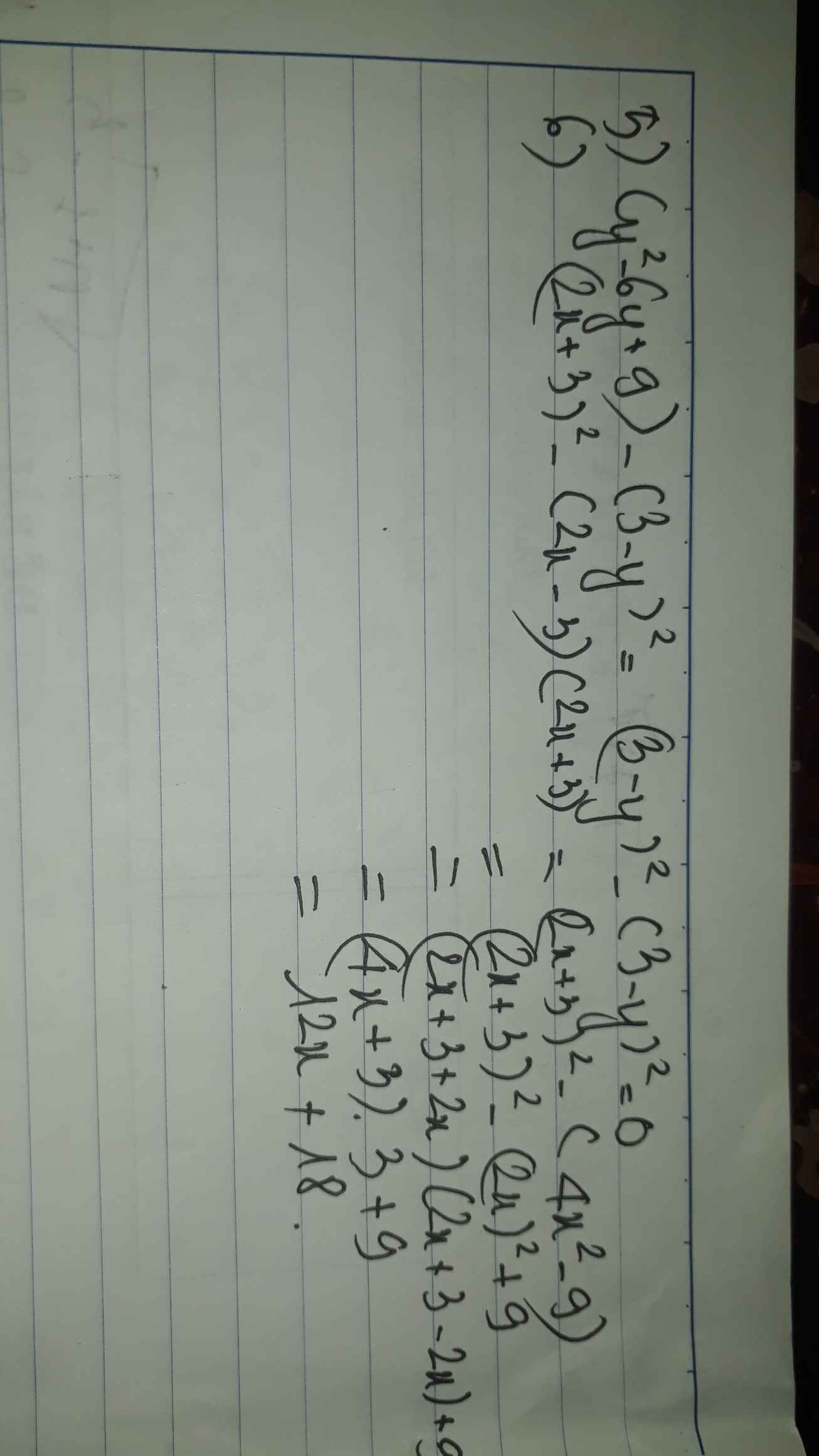
đề là ptđt thành nhân tử hả bạn ?
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(x^2+7x+10=t\)
\(t\left(t+2\right)-24=t^2+2t-24=\left(t-4\right)\left(t+6\right)\)
Theo cách đặt : \(\left(x^2+7x+6\right)\left(x^2+7x+16\right)=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x+2\right)\left(x+5\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(x^2+7x+11=t\)
\(\Rightarrow\left(t+1\right)\left(t-1\right)-24\)
\(=t^2-1-24\)
\(=t^2-25\)
\(=\left(t-5\right)\left(t+5\right)\)
\(\Rightarrow\left(x^2+7x+11-5\right)\left(x^2+7x+11+5\right)\)
\(=\left(x^2+7x+6\right)\left(x^2+7x+16\right)\)
\(=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)