Tìm \(x,\) \(y\) sao cho:
\(B=-x^2+2xy-4y^2+2x+10y-8\) có \(GTLN\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BS
1
TC
Trên con đường thành công không có....
24 tháng 8 2021
Đúng(0)
Những câu hỏi liên quan
ML
18 tháng 7 2015
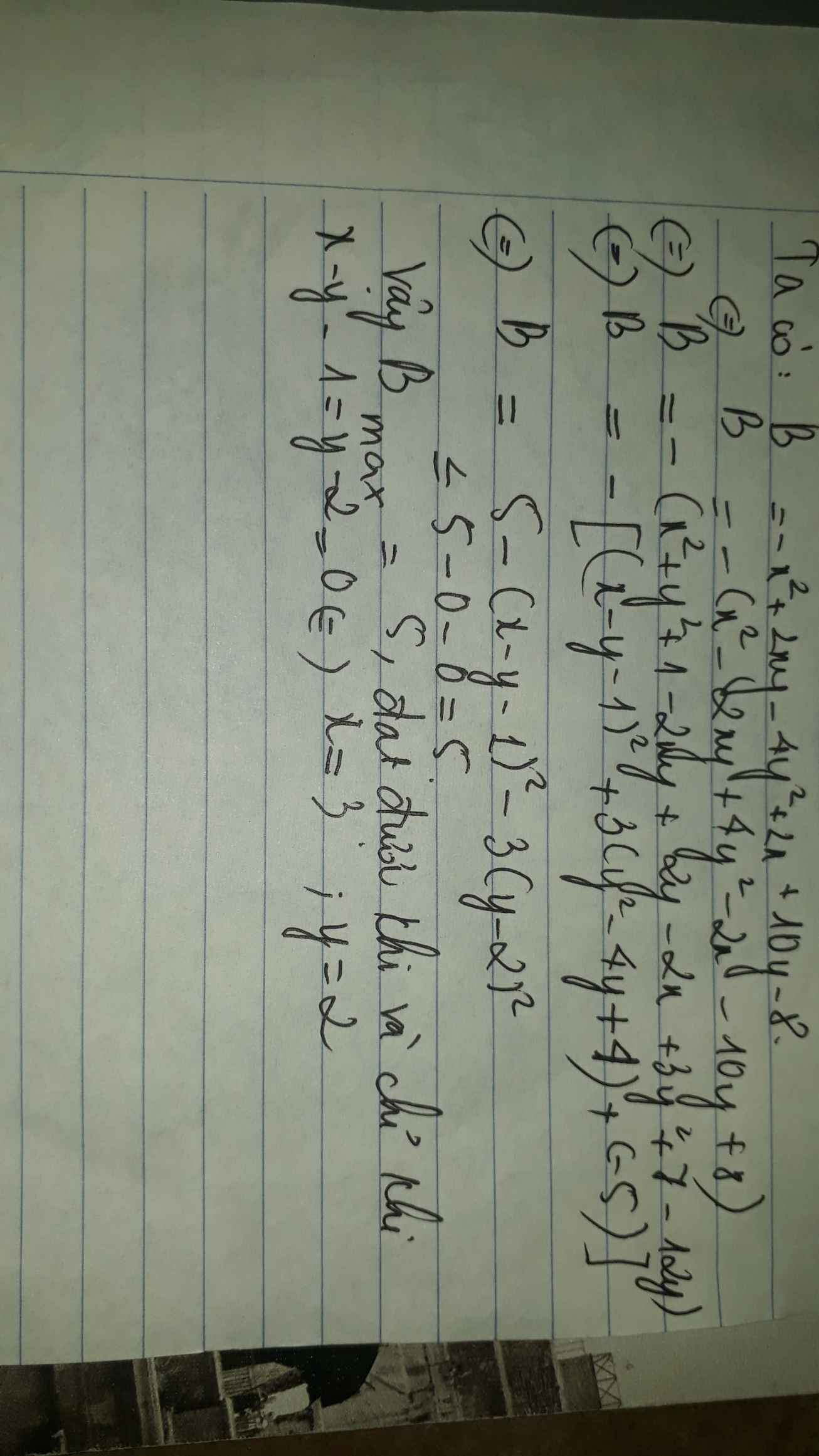
\(6B=-6x^2+12xy-24y^2+12x+60y-48\)
\(=\left(-4x^2+12xy-9y^2\right)+\left(-2x^2+12x\right)+\left(-15y^2+60y\right)-48\)
\(=-\left(2x-3y\right)^2-2\left(x^2-6x+9\right)-15\left(y^2-4y+4\right)+30\)
\(=-\left(2x-3y\right)^2-2\left(x-3\right)^2-15\left(y-2\right)^2+30\le30\)
Dấu "=" xảy ra khi \(2x-3y=0;\text{ }x-3=0;\text{ }y-2=0\Leftrightarrow x=3;\text{ }y=2\)
Vậy GTLN của B là \(\frac{30}{8}=5\) tại x = 3; y = 2.
AM
6
14 tháng 1 2016
B=-x^2+2xy-4y^2+2x+10y-8
B = (-x^2 - y^2 - 1 + 2xy + 2x - 2y) + (-3y^2 + 12y - 12) + 5
B = -(x^2+y^2+1 - 2xy - 2x + 2y) - 3(y^2 - 4y + 4) + 5
B = - (x - y - 1)^2 - 3(y - 2)^2 +5 5
Max B = 5 khi x = 3, y = 2
25 tháng 6 2017
B=-x^2+2xy-4y^2+2x+10y-8
B= x^2-2xy+4y^2-2x-10y+8
B= ( x^2+y^2+1-2xy-2x+2y) +(3y^2-12y+7)
B=(x-y-1)^2+ 3(y^2-4y+7/4)=(x-y-1)^2+3(y-2)^2-27/4>=-... nen A<= 27/4
ban tu tim dau = nhe
T
7 tháng 8 2016
kí hiệu a l b là a chia hết cho b nhé
xy-1 l (x-1)(y-1) <=> xy-1 l y-1 <=> y(x-1)+y-1 l y-1 => x-1 l y-1
tương tự : y-1 l x-1
=> \(\orbr{\begin{cases}x-1=y-1\\x-1=1-y\end{cases}}\Rightarrow\orbr{\begin{cases}x=y\\x+y=2\end{cases}}\)
+> x=y \(\Rightarrow x^2-1\)l \(\left(x-1\right)^2\) <=> x+1 l x-1 <=> 2 l x-1 => x=2 hoặc x=3
|+> x+y=2 thay vào tương tự như trên nhé
28 tháng 8 2018
\(A=-x^2+2xy-4y^2+2x+10y-8\)
\(=-\left(x^2-2xy+4y^2-2x-10y+8\right)\)
\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2-5\right]\)
\(=5-\left(x-y-1\right)^2-3\left(y-2\right)^2\le5\)
Dấu"=" xảy ra <=> \(\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}\) <=> \(\hept{\begin{cases}x=3\\y=2\end{cases}}\)
Vậy MAX \(A=5\)khi \(x=3;\)\(y=2\)
T
9 tháng 8 2017
a) \(M=10x^2+6y+4y^2+4xy+2\)
\(=\left(10x^2+4xy+\dfrac{2}{5}y^2\right)+\left(\dfrac{18}{5}y^2+6y+\dfrac{5}{2}\right)-\dfrac{1}{2}\)
\(=10\left(x^2+\dfrac{2}{5}xy+\dfrac{1}{25}y^2\right)+\dfrac{18}{5}\left(y^2+\dfrac{5}{3}y+\dfrac{25}{36}\right)-\dfrac{1}{2}\)
\(=10\left(x+\dfrac{1}{5}y\right)^2+\dfrac{18}{5}\left(y+\dfrac{5}{6}\right)^2-\dfrac{1}{2}\ge-\dfrac{1}{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{5}y=0\\y+\dfrac{5}{6}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=-\dfrac{5}{6}\end{matrix}\right.\)
b) \(H=-x^2+2xy-4y^2+2x+10y-8\)
\(=-x^2+2x\left(y+1\right)-\left(y^2+2y+1\right)-\left(3y^2-12y+7\right)\)
\(=-x^2+2x\left(y+1\right)-\left(y+1\right)^2-3\left(y^2-4y+4\right)+5\)
\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\le5\)
Đẳng thức xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
c) \(K=2x^2+2xy-2x+2xy+y^2\)
bn xem lại cái đề nhé, sao lại có 2 lần 2xy