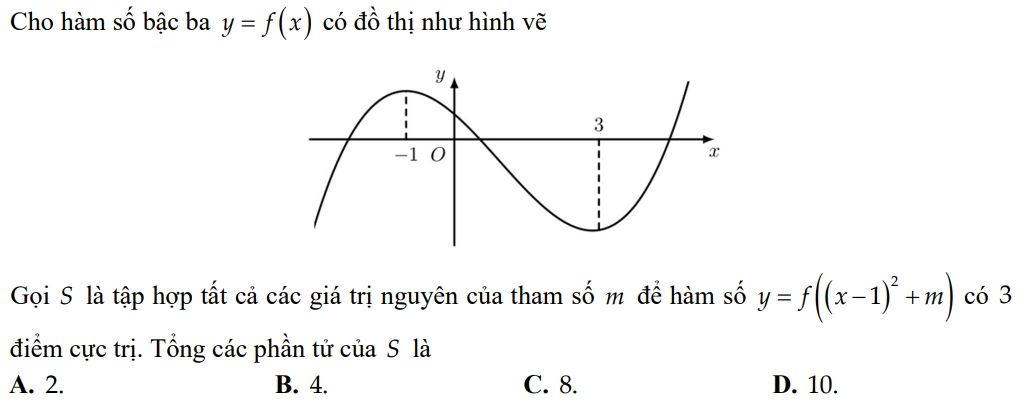
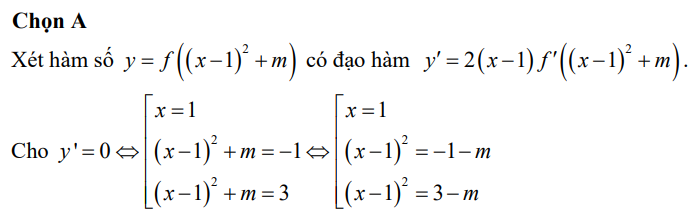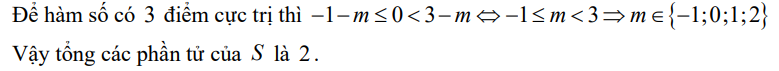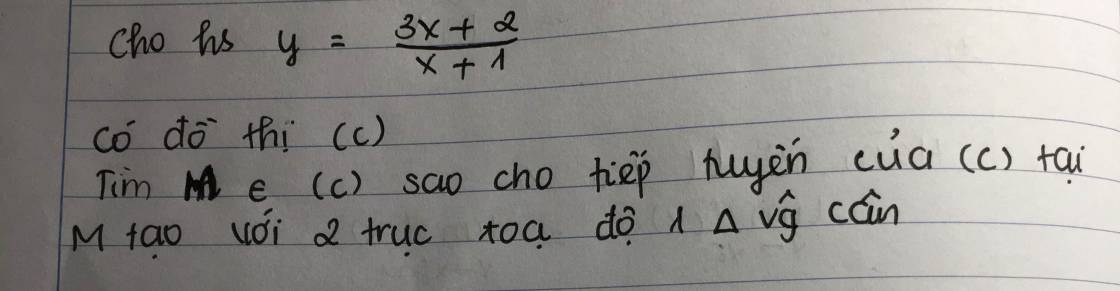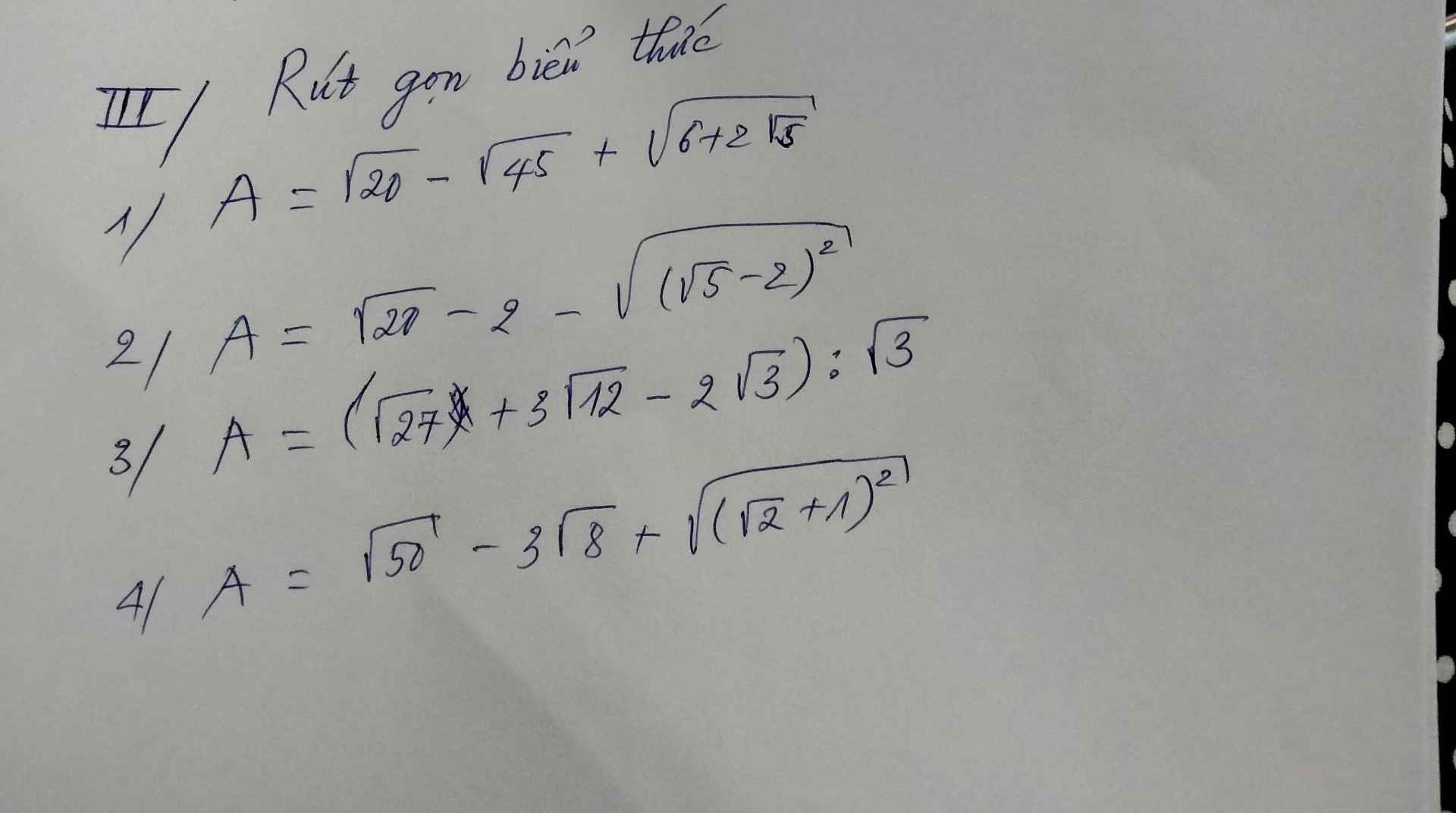Giúp mình bài 1 với mng ơi. mình không hiểu😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
29 tháng 5 2023
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
PB
2
2
10 tháng 5 2023
`y'=[3(x+1)-3x-2]/[(x+1)^2]=1/[(x+1)^2]`
Gọi `M(x_0; y_0)-` tiếp điểm
Mà `y_0=[3x_0+2]/[x_0+1] in T T`
`=>y-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`@` Gọi `T T nn Ox =A`
`=>-[3x_0+2]/[x_0+1]=1/[(x_0+1)^2](x-x_0)`
`<=>(-3x_0 -2)(x_0+1)=x-x_0`
`<=>-3x_0 ^2-3x_0 -2x_0 -2=x-x_0`
`<=>x=-3x_0 ^2-4x_0 -2`
`=>OA=|-3x_0 ^2-4x_0 -2|`
`@` Gọi `T T nn Oy=B`
`=>y-[3x_0 +2]/[x_0 +1]=1/[(x_0 +1)^2](-x_0)`
`<=>y=[(3x_0+2)(x_0+1)-x_0]/[(x_0+1)^2]`
`<=>y=[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]`
`=>OB=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
Vì `\triangle OAB` vuông cân tại `O`
`=>OA=OB`
`<=>|-3x_0 ^2-4x_0 -2|=|[3x_0 ^2+4x_0 +2]/[(x_0 +1)^2]|`
`<=>(x_0+1)^2=1`
`<=>[(x_0=0),(x_0=-2):}`
`=>` PTTT: `[(y=x+2),(y=x+6):}`
ND
1
DT
19 tháng 12 2022
\(n_{NO}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
\(3R+8HNO_3\rightarrow3R\left(NO_3\right)_2+2NO+4H_2O\)
từ pthh suy ra: \(n_R=\dfrac{3}{2}.n_{NO}=\dfrac{3}{2}.0,1=0,15\left(mol\right)\)
=> \(M_R=\dfrac{9,75}{0,15}=65\)
Vậy tên của R: kẽm (Zn)
LM
Lê Minh Vũ
CTVHS
10 tháng 6 2023
Mình tính từng cái ra nha, từng cái sẽ ra được kết quả của phép tính:
\(1-\dfrac{1}{5}-\dfrac{1}{6}\)
\(=\left(1-\dfrac{1}{5}\right)-\dfrac{1}{6}\)
\(=\left(\dfrac{5}{5}-\dfrac{1}{5}\right)-\dfrac{1}{6}\)
\(=\dfrac{4}{5}-\dfrac{1}{6}\)
\(=\dfrac{24}{30}-\dfrac{5}{30}\)
\(=\dfrac{19}{30}\)
J
3
Y
28 tháng 6 2023
\(a,A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(=x-0,2-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(=\left(-0,2-2+2\right)+\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)\)
\(=-0,2\)
\(b,B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(=x^3-8y^3-x^3+8y^3-10\)
\(=-10\)
\(c,C=4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)-4x\)
\(=4\left(x^2+2x+1\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=13\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 6 2023
a) \(A=0,2\left(5x-1\right)-\dfrac{1}{2}\left(\dfrac{2}{3}x+4\right)+\dfrac{2}{3}\left(3-x\right)\)
\(A=x-\dfrac{1}{5}-\dfrac{1}{3}x-2+2-\dfrac{2}{3}x\)
\(A=\left(x-\dfrac{1}{3}x-\dfrac{2}{3}x\right)-\left(\dfrac{1}{5}+2-2\right)\)
\(A=-\dfrac{1}{5}\)
Vậy: ...
b) \(B=\left(x-2y\right)\left(x^2+2xy+4y^2\right)-\left(x^3-8y^3+10\right)\)
\(B=\left[x^3-\left(2y\right)^3\right]-\left[x^3-\left(2y\right)^3\right]-10\)
\(B=-10\)
Vậy: ...
c) \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x+1\right)\left(x-1\right)-4x\)
\(=4\left(x^2+2x+4\right)+\left(4x^2-4x+1\right)-8\left(x^2-1\right)-4x\)
\(=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\)
\(=\left(4x^2+4x^2-8x^2\right)+\left(8x-4x-4x\right)+\left(4+1+8\right)\)
\(=13\)
Vậy:...
10 tháng 12 2021
IV:
1.playing
2.was perform
3.visited
4.watching
5.for join-accompanied
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}=\sqrt{2^2.5}-\sqrt{3^2.5}+\sqrt{\left(\sqrt{5}+1\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1=1\)
\(\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}=2\sqrt{5}-2-\left|\sqrt{5}-2\right|=2\sqrt{5}-2-\sqrt{5}+2=\sqrt{5}\)
\(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}=7\sqrt{3}:\sqrt{3}=7\)
\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{5^2.2}-3\sqrt{2^2.2}+\sqrt{\left(\sqrt{2}+1\right)^2}=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1=1\)
2 tháng 8 2021
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1\)
=1
2) Ta có: \(B=\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=2\sqrt{5}-2-\sqrt{5}+2\)
\(=\sqrt{5}\)