Question

[Nguyễn Hoàng Bảo Nhi]

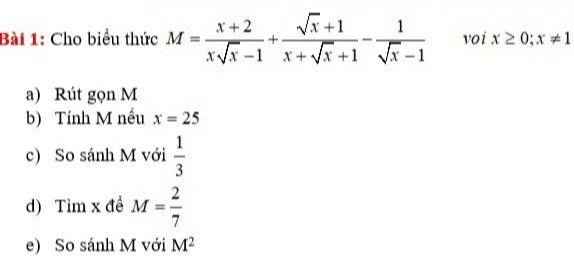
Giúp mình đy mọi ng càng nhanh càng tốt đang cần gấp!

Answer 1

[Yeutoanhoc]

`a)M=(x+2)/(xsqrtx-1)+(sqrtx+1)/(x+sqrtx+1)-1/(sqrtx-1)(x>=0,x ne 1)`

`M=(x+2)/((sqrtx-1)(x+sqrtx+1))+((sqrtx+1)(sqrtx-1))/((sqrtx-1)(x+sqrtx+1))-(x+sqrtx+1)/((sqrtx-1)(x+sqrtx+1))`

`M=(x+2+x-1-x-sqrtx-1)/((sqrtx-1)(x+sqrtx+1))`

`M=(x-sqrtx)/((sqrtx-1)(x+sqrtx+1))`

`M=(sqrtx(sqrtx-1))/((sqrtx-1)(x+sqrtx+1))`

`M=sqrtx/(x+sqrtx+1)`

`b)x=25(tmđk)`

`=>sqrtx=5`

`=>M=5/(25+5+1)`

`=>M=5/31`

`c)M=sqrtx/(x+sqrtx+1)`

`x=0=>M=0<1/3`

`x>0=>M=1/(sqrtx+1+1/sqrtx)`

Áp dụng bđt cosi:

`sqrtx+1/sqrtx>=2`

`=>sqrtx+1+1/sqrtx>=3>0`

`=>M<=1/3`

Dấu "=" xảy ra khi `sqrtx=1/sqrtx<=>x=1`(KTMĐKXĐ)

`=>M<1/3`

Vậy `M<1/3`

`d)M=2/7`

`<=>sqrtx/(x+sqrtx+1)=2/7`

`<=>2x+2sqrtx+2=7`

`<=>2x-5sqrtx+2=0`

`<=>2x-4sqrtx-sqrtx+2=0`

`<=>(sqrtx-2)(2sqrtx-1)=0`

`<=>[(sqrtx=2),(2sqrtx=1):}`

`<=>[(x=4),(x=1/4):}(TMĐK)`

`e)` Vì `x>=0=>sqrtx>=0`

`=>x+sqrtx+1>=1>0`

`=>M>=0`

Mặt khác:`M<1/3`(câu b)

`=>M<1=>M-1<0`

`=>M(M-1)<=0`

`<=>M^2-M<=0`

`<=>M^2<=M`

Answer 2

[Nguyễn Lê Phước Thịnh]

a: Ta có: \(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)

\(=\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

b: Thay x=25 vào M, ta được:

\(M=\dfrac{5}{25+5+1}=\dfrac{5}{31}\)

c: Ta có: \(M-\dfrac{1}{3}\)

\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)

\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{-\left(x-2\sqrt{x}+1\right)}{3\left(x+\sqrt{x}+1\right)}\)

\(=\dfrac{-\left(\sqrt{x}-1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\forall x\) thỏa mãn ĐKXĐ

hay \(M< \dfrac{1}{3}\)