cho hai hình bình hành ABCD và A'BC'D' có chúng đỉnh b .
a)chứng minh rằng DD'=AA'+CC'
b)tam giác ACD' và A'C'D có cùng trọng tâm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔMEA và ΔMCB có
góc EMA=góc CMB
MA=MB
góc MEA=góc MCB
=>ΔMEA=ΔMCB
=>ME=MC
=>M là trung điểm của CE
Xét tứ giác AEBC có
M là trung điểm chung của AB và EC
=>AEBC là hbh
b: Để AEBC là hình chữ nhật thì góc EAC=90 độ
=>góc DAC=90 độ
=>góc ACD+góc D=90 độ
mà góc ACD=1/2*góc D
nên góc D=2/3*90=60 độ
=>góc B=60 độ
góc BAD=góc BCD=180-60=120 độ

Cách 1:
Nhìn hình ta có: AD = BC = 8cm; BM = ND = 4cm
nên diện tích tam giác AND = diện tích tam giác BMC.
Diện tích tam giác AND là:
4 × 8 : 2 = 16 ( c m 2 )
Diện tích hình chữ nhật ABCD là
10 × 8 = 80 ( c m 2 )
Diện tích hình bình hành AMCN là:
Diện tích hình chữ nhật ABCD + diện tích tam giác AND + diện tích tam giác BCM = 80 + 16 + 16 = 112 (cm2)
Cách 2:
Nối hai điểm AC ta được 2 tam giác bằng nahu CAN = ACM
Với NC = AM = 14cm là hai cạnh đáy của 2 tam giác trên
Diện tích tam giác CAN là:
14 × 8 : 2 = 56 ( c m 2 )
Diện tích hình bình hành AMCN là:
56 × 2 =112 ( c m 2 )

Vì hình bình hành ABCD có 2 cạnh liền kề bằng nhau AB = BC nên ABCD là hình thoi
Suy ra: AB = BC = CD= DA = 10cm và O là trung điểm của AC và trung điểm của BD
Ta có: AC = 2AO = 2. 6 = 12cm
Áp dụng định lí py tago vào tam giác AOD có:
A D 2 = A O 2 + O D 2 suy ra: O D 2 = A D 2 – A O 2 = 10 2 – 6 2 = 64 nên OD = 8cm
Suy ra: BD = 2OD = 16cm
Diện tích hình thoi ABCD là:
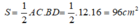
Chọn đáp án A

Hình bình hành ABCD có chu vi là 80cm, độ dài cạnh AB = 25 cm . Vậy độ dài BC là
A. 15 cm C. 40Cm
C. 55cm D. 28cm
cho em hỏi lại câu này với ạ

bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình

Ta có: \(\widehat{FAH}+\widehat{BAD}+\widehat{BAF}+\widehat{HAD}=360^0\)
=>\(\widehat{FAH}+\widehat{BAD}+90^0+90^0=360^0\)
=>\(\widehat{FAH}+\widehat{BAD}=180^0\)
mà \(\widehat{BAD}+\widehat{ABC}=180^0\)(ABCD là hình bình hành)
nên \(\widehat{FAH}=\widehat{ABC}\)
ABEF là hình vuông
=>AB=AF
AHGD là hình vuông
=>AH=AD
mà AD=BC
nên AH=BC
Xét ΔFAH và ΔABC có
FA=AB
\(\widehat{FAH}=\widehat{ABC}\)
AH=BC
Do đó:ΔFAH=ΔABC
=>AC=FH và \(\widehat{AFH}=\widehat{BAC}\); \(\widehat{ACB}=\widehat{AHF}\)
Gọi K là giao điểm của HF với AC
Ta có: \(\widehat{KAH}+\widehat{HAD}+\widehat{DAC}=180^0\)
=>\(\widehat{KAH}+\widehat{DAC}+90^0=180^0\)
=>\(\widehat{KAH}+\widehat{DAC}=90^0\)
mà \(\widehat{DAC}=\widehat{ACB}\) và \(\widehat{ACB}=\widehat{AHF}\)
nên \(\widehat{KAH}+\widehat{AHF}=90^0\)
=>ΔKAH vuông tại K
=>AK\(\perp\)HF tại K
=>AC\(\perp\)FH tại K

Chọn đáp án A
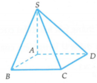
Ta có ABCD là hình bình hành nên CD//AB.
Lại có S A ⊥ A B C D ⇒ S A ⊥ A B
⇒ ∆ S A B vuông tại A.
Suy ra
![]()
Trong tam giác SAB vuông tại A có
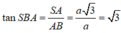
⇒ S B A ⏜ = 60 0