Câu 1: (4,0 điểm) Tính hợp lý
a) \(\dfrac{-7}{25}+\dfrac{-18}{25}+\dfrac{4}{23}+\dfrac{5}{7}+\dfrac{19}{23}\)
b)\(\dfrac{7}{19}.\dfrac{8}{11}+\dfrac{7}{19}.\dfrac{3}{11}+\dfrac{12}{19}\)
c)\(\left(-25\right).125.4.\left(-8\right).\left(-17\right)\)
d) \(\dfrac{7}{35}.\dfrac{10}{19}+\dfrac{7}{35}.\dfrac{9}{19}-\dfrac{2}{35}\)
Câu 2: (3,0 điểm)
Tính giá trị các biểu thức sau
a. \(A=\dfrac{1}{2}\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)...\left(1+\dfrac{1}{2015.2017}\right)\)
b.\(B=2x^2-3x+5\) với \(\left|x\right|=\dfrac{1}{2}\)
c. \(C=2x-2y+13x^3y^2\left(x-y\right)+15\left(y^2x-x^2y\right)+\left(\dfrac{2015}{2016}\right)^0\), biết x-y=0
Câu 3(4,0 điểm0
1.Tìm x,y biết : \(\left(2x-\dfrac{1}{6}\right)^2+\left|3y+12\right|\le0\)
2.Tìm x,y,z biết : \(\dfrac{3x-2y}{4}=\dfrac{2z-4x}{3}=\dfrac{4y-3z}{2};x+y+z=18\)
Câu 4: (3,0 điểm)
1. Tìm các số nguyên x,y biết : \(x-2xy+y-3=0\)
2. Cho đa thức f(x)=\(x^{10}-101x^9+101x^8-101x^7+...-101x+101.\)
Tính f(100)
Câu 5 (5,0 điểm)
Cho tam giác ABC có ba góc nhọn (AB<AC).Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE.Gọi I là giao điểm của CD và BE,K là giao điểm của AB và DC
a) Chứng minh rằng : tam giác ADC=tam giác ABE
b)Chứng minh rằng : góc DIB=60 độ
c) Gọi M và N lần lượt là trung điểm của CD và BE.Chứng minh rằng tam giác AMN là tam giác đều
d)Chứng minh rằng IA là phân giác của góc DIE
Câu 6: (1,0 điểm)
Cho tam giác ABC vuông tại A có AB=3cm,AC=4cm.Điểm I nằm trong tam giác và cách đều 3 cạnh tam giác ABc.Gọi M là chân đường vuông góc kẻ từ I đến BC.Tính MB
@Hồng Phúc Nguyễn

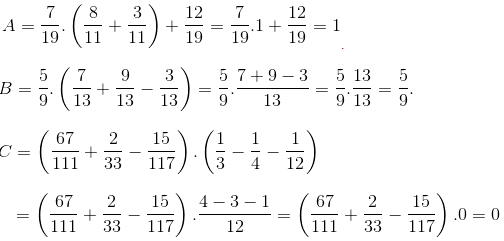
Đề hsg hả?
Nguyễn Phương Trâm ừ