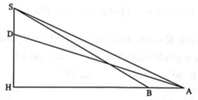
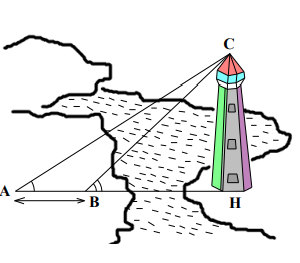
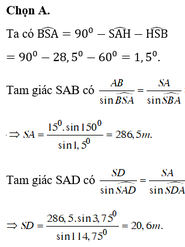Hai xạ thủ đang ở hai vị trí A và B. Họ cần tiêu diệt một tên khủng bố IS đang bắt giữ con tin trên đỉnh ngọn tháp (vị trí C). Biết rằng hai xạ thủ cách nhau 38m và các góc với số đo như sau: HAC = 34o ; HBC = 52o và ba điểm A, B, H thẳng hàng. Xạ thủ A bắn trước và chỉ trong một phát đạn đã tiêu diệt được mục tiêu. Tính độ dài đường đạn của xạ thủ A (đường đạn bay thẳng, bỏ qua độ quay của Trái đất và sức cản ngang của gió). (Làm tròn hai chữ số thập phân)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Áp dụng tỉ số lượng giác vào tam giác ABC vuông tại B
\(\Rightarrow tan60=\dfrac{h}{BC}\)
\(\Rightarrow BC=\dfrac{h\sqrt{3}}{3}\)
\(\Rightarrow BD=BC+CD=\dfrac{h\sqrt{3}}{3}+600\)
- Áp dụng tỉ số lượng giác vào tam giác ABD vuông tại B
\(tan50=\dfrac{h}{BD}\)
\(\Rightarrow h=tan50.\left(\dfrac{h\sqrt{3}}{3}+600\right)\)
\(\Rightarrow h\approx2292m\)
Vậy ...

Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.

Câu 3:
Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)
=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)
=>\(CA\simeq183,85\left(m\right)\)
Câu 4:
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔABE vuông tại A có AC là đường cao
nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)
b: Ta có: ΔOAD cân tại O
mà OE là đường cao
nên OE là phân giác của góc AOD
Xét ΔOAE và ΔODE có
OA=OD
\(\widehat{AOE}=\widehat{DOE}\)
OE chung
Do đó: ΔOAE=ΔODE
=>\(\widehat{OAE}=\widehat{ODE}=90^0\)
Xét tứ giác EAOD có
\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
=>EAOD là tứ giác nội tiếp
=>E,A,O,D cùng thuộc một đường tròn
c: Xét (O) có
OD là bán kính
ED\(\perp\)DO tại D
Do đó: ED là tiếp tuyến của (O)
Xét (O) có
\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC
\(\widehat{CBD}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{EDC}=\widehat{CBD}\)
=>\(\widehat{EDC}=\widehat{EBD}\)
Xét ΔEDC và ΔEBD có
\(\widehat{EDC}=\widehat{EBD}\)
\(\widehat{DEC}\) chung
Do đó: ΔEDC đồng dạng với ΔEBD
=>\(\widehat{ECD}=\widehat{EDB}\)


Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
![]()
Xét tam giác ADC vuông tại C có:
![]()
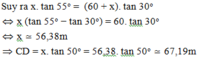
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
 Hình
Hình