Với x>2 tìm GTNN của y = x + \(\dfrac{2x+5}{x-2}\) Giúp mình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
3 tháng 5 2023
Mình nghĩ ra câu C rồi bạn nào giúp mình nghĩ nốt câu A,B hộ mình nhé mình cảm ơn!
11 tháng 5 2023
a:6x-5-9x^2
=-(9x^2-6x+5)
=-(9x^2-6x+1+4)
=-(3x-1)^2-4<=-4
=>A>=2/-4=-1/2
Dấu = xảy ra khi x=1/3
b: \(B=\dfrac{4x^2-6x+4-1}{2x^2-3x+2}=2-\dfrac{1}{2x^2-3x+2}\)
2x^2-3x+2=2(x^2-3/2x+1)
=2(x^2-2*x*3/4+9/16+7/16)
=2(x-3/4)^2+7/8>=7/8
=>-1/2x^2-3x+2<=-1:7/8=-8/7
=>B<=-8/7+2=6/7
Dâu = xảy ra khi x=3/4
9 tháng 8 2023
a: \(E=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{\left(x+1\right)\left(x-1\right)+x+2-x^2}{x\left(x-1\right)}\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x^2-1+x+2-x^2}\)
\(=\dfrac{x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{x-1}\)
c: |2x+1|=5
=>2x+1=5 hoặc 2x+1=-5
=>x=-3(nhận) hoặc x=2(nhận)
Khi x=-3 thì \(E=\dfrac{\left(-3\right)^2}{-3-1}=-\dfrac{9}{4}\)
Khi x=2 thì \(E=\dfrac{2^2}{2-1}=4\)
DD
2
22 tháng 10 2021
Áp dụng BĐT cosi:
\(A=\left(3x+\dfrac{3}{x}\right)+\left(\dfrac{4}{9}y+\dfrac{4}{y}\right)+\left(2x+y\right)\\ A\ge2\sqrt{\dfrac{9x}{x}}+2\sqrt{\dfrac{16y}{9y}}+5\\ A\ge2\cdot3+2\cdot\dfrac{4}{3}+5=\dfrac{41}{3}\)
Vậy \(A_{min}=\dfrac{41}{3}\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{3}{x}\\\dfrac{4y}{9}=\dfrac{4}{y}\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
1 tháng 1 2021
Ta có: \(\left(x-1\right)^2+\left(x+y\right)^2\le9\Rightarrow x+y\le3\).
Áp dụng bất đẳng thức AM - GM ta có:
\(\dfrac{2}{x}+2x\ge2\sqrt{\dfrac{2}{x}.2x}=4;\dfrac{4}{y}+y\ge2\sqrt{\dfrac{4}{y}.y}=4\).
Do đó \(\dfrac{2}{x}\ge4-2x;\dfrac{4}{y}\ge4-y\)
\(\Rightarrow P\ge8-4\left(x+y\right)\ge-4\). (do \(x+y\le3\)).
Vậy...
Đẳng thức xảy ra khi và chỉ khi x = 1; y = 2.
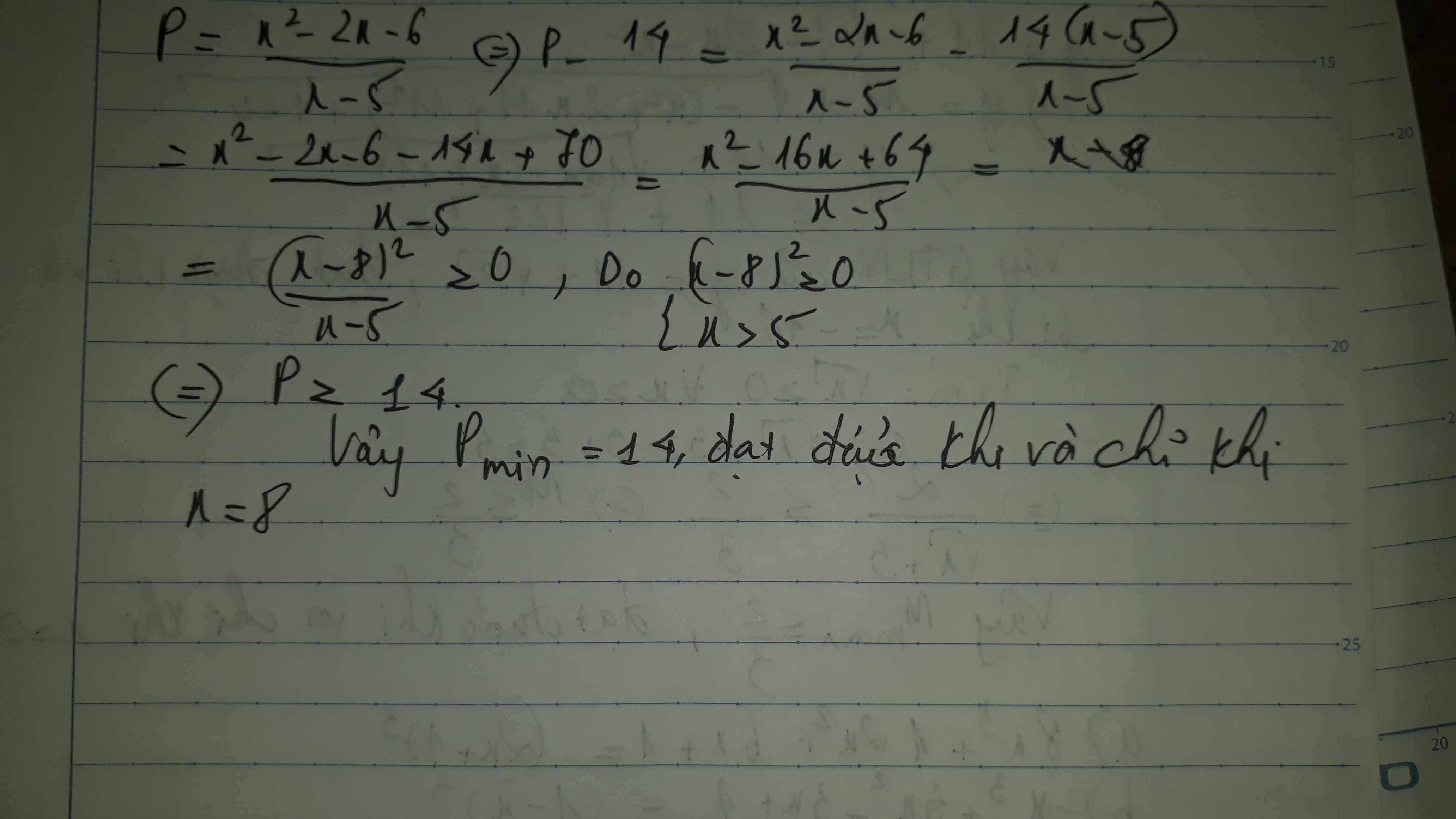
Vì x>2 áp dụng BĐT Cauchy cho 2 số dương
\(y=x+\dfrac{2x+5}{x-2}=x+\dfrac{2x-4+9}{x-2}=x+2+\dfrac{9}{x-2}\)
\(=6+\left(x-2+\dfrac{9}{x-2}\right)\ge6+2\sqrt{x-2.\dfrac{9}{x-2}}=6+2\sqrt{9}=10\)
Đẳng thức xảy ra \(\Leftrightarrow x-2=\dfrac{9}{x-2}\Leftrightarrow x=5\)