đố ai giải được bài này
Xy+xx+yx+yy (X+y)x21
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
0
12 tháng 3 2018
Đề phải cho x,y thuộc Z nha bạn
pt <=> (x-y)^3 = xy+8-3xy.(x-y)
<=> (x-y)^3 = 8 - xy.(3x-3y-1)
<=> (3x-3y)^3 = 216 - 27.(3x-3y-1)
<=> (3x-3y)^3 - 1 = 215 - 27.(3x-3y-1)
Đến đó bạn tự phân tích thành nhân tử có VP = 215 mà giải nha
CM
26 tháng 1 2019
Chọn đáp án C.
Vì x, y ,z > 0 nên x + y > 0; y + z > 0 và x + z > 0
Ta có:
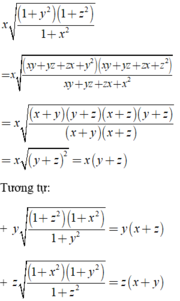
Khi đó
A = x(y + z) + y(x + z) + z(x + y)
= xy + xz + xy + yz + xz + zy = 2(xy + yz + zx) = 2
LM
3
10 tháng 1 2016
10).(X,Y).(10).(9,9)=100.(XX,YY)
(XY).(99)=(XXYY)
(10X+Y).(99)=1000X+100X+10Y+Y
990X+99Y=1100X+11Y
88Y=110X
(88:22).Y=(110:22)X
4. Y=5 .X <=>
Y=5 ; X=4
4,5 x 9,9 = 44,55
VN
6
23 tháng 11 2017
Mình nghi đề sai ; nếu đề có đúng giải như sau
Ta có : \(4P=4x^2+4y^2+4xy-4x-4y+8\)
\(=\left(4x^2+4xy+y^2\right)-\left(4x+2y\right)+1+\left(3y^2-2y+\frac{1}{3}\right)+\frac{20}{3}\)
\(=\left(2x+y\right)^2-2\left(2x+y\right)+1+3\left(y^2-\frac{2}{3}y+\frac{1}{9}\right)+\frac{20}{3}\)
\(=\left(2x+y-1\right)^2+3\left(y-\frac{1}{3}\right)^2+\frac{20}{3}\)
Ta thấy \(\left(2x+y-1\right)^2+3\left(y-\frac{1}{3}\right)^2\ge0\forall x;y\)
\(\Rightarrow4P=\left(2x+y-1\right)^2+3\left(y-\frac{1}{3}\right)^2+\frac{20}{3}\ge\frac{20}{3}\forall x;y\)
\(\Rightarrow P\ge\frac{20}{3}:4=\frac{20}{12}=\frac{5}{3}\)
Đẳng thức xảy ra \(\Leftrightarrow x=y=\frac{1}{3}\)
Vậy \(P_{min}=\frac{5}{3}\) tại \(x=y=\frac{1}{3}\)
PT
1
