tìm n thuộc z để 2n2-n+2 chia het cho 2n+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
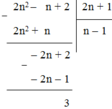
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
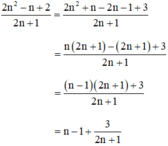
2n2 – n + 2 chia hết cho 2n + 1
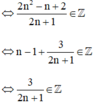
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.

Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
2n^2 - n + 2 2n + 1 n - 1 _ 2n^2 + n -2n + 2 _ -2n - 1 3
2n2 – n + 2 chia hết cho 2n + 1
<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)
<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }
+ 2n + 1 = 1 <=> 2n = 0 <=> n = 0
+ 2n + 1 = -1 <=> 2n = -2 <=> n = -1
+ 2n + 1 = 3 <=> 2n = 2 <=> n = 1
+ 2n + 1 = -3 <=> 2n = -4 <=> n = -2.
Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }

\(2n^2-n+2⋮2n+1\)
\(2n^2+n-2n-1+3⋮2n+1\)
\(n\left(2n+1\right)-\left(2n+1\right)+3⋮2n+1\)
\(\left(2n+1\right)\left(n-1\right)+3⋮2n+1\)
Vì \(\left(2n+1\right)\left(n-1\right)⋮2n+1\)
\(\Rightarrow3⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(3\right)=\left\{1;3;-1;-3\right\}\)
\(\Rightarrow n\in\left\{0;1;-1;-2\right\}\)
Vậy.........

2n2+5n-1=n(2n-1)+6n-1
=n(2n-1)+3(2n-1)+2
do 2n2+5n-1 chia hết cho 2n-1 => 2 chia hết cho 2n-1
=> 2n-1 thuộc tập ước của 2 là 1;2
=> n=1 (TM) n=1,5 (loại)

Ta có
n+6 chia hết cho n-3
=> n-3 +9 chia hết cho n-3
Vì n-3 chia hết cho n-3
=> 9 chia hết cho n-3
Xét các ước của 9 để tìm đk n là số tự nhiên
Ta có:
2n+8 chia hết cho n+2
=>2(n+2)+4 chia hết cho n+2
Các phần sau làm tương tự câu trên
Ta có
3n+5 chia hết cho -2n+1
=> 3n+5 chia hết cho 2n-1
=> 6n+10 chia hết cho 2n-1
=>3(2n-1)+13 chia hết cho 2n-1
Phần sau làm tương tự nhé bạn

3n chia hết cho 5- 2n
=>2.3n chia hết cho 2.(5-2n)
=>6n chia hết cho 10-6n
=>6n-10+10 chia hết cho 10-6n
=>-(10-6n)+10 chia hết cho 10-6n
=>10 chia hết cho 10-6n
=>10-6n thuộc Ư(10)={1;-1;2;-2;5;-5;10;-10}
ta có bảng sau:
| 10-6n | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| n | 3/2(loại) | 11/6(loại) | 1(TM) | 2(TM) | 5/6(loại) | 15/6(loại) | 0(TM) | 10/3(loại) |
Vậy n={1;2;0}
4n + 3 chia het cho 2n+6
=>4n+12-9 chia hết cho 2n+6
=>2.(2n+6)-9 chia hết cho 2n+6
=>9 chia hết cho 2n+6
=>2n+6 thuộc Ư(9)={1;-1;3;-3;9;-9}
ta có bảng sau:
| 2n+6 | 1 | -1 | 3 | -3 | 9 | -9 |
| n | -5/2(loại) | -7/2(loại) | -3/2(loại) | -9/2(loại) | 3/2(loại) | -15/2(loại) |
Vậy n=\(\phi\)
3n chia hết cho 5- 2n
=>2.3n chia hết cho 2.(5-2n)
=>6n chia hết cho 10-6n
=>6n-10+10 chia hết cho 10-6n
=>-(10-6n)+10 chia hết cho 10-6n
=>10 chia hết cho 10-6n
=>10-6n thuộc Ư(10)={1;-1;2;-2;5;-5;10;-10}
ta có bảng sau:
| 10-6n | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| n | 3/2(loại) | 11/6(loại) | 1(TM) | 2(TM) | 5/6(loại) | 15/6(loại) | 0(TM) | 10/3(loại) |
Vậy n={1;2;0}
4n + 3 chia het cho 2n+6
=>4n+12-9 chia hết cho 2n+6
=>2.(2n+6)-9 chia hết cho 2n+6
=>9 chia hết cho 2n+6
=>2n+6 thuộc Ư(9)={1;-1;3;-3;9;-9}
ta có bảng sau:
| 2n+6 | 1 | -1 | 3 | -3 | 9 | -9 |
| n | -5/2(loại) | -7/2(loại) | -3/2(loại) | -9/2(loại) | 3/2(loại) | -15/2(loại) |
Vậy n=\(\phi\)

1:
2n^2+5n-1 chia hết cho 2n-1
=>2n^2-n+6n-3+2 chia hết cho 2n-1
=>2n-1 thuộc {1;-1;2;-2}
mà n nguyên
nên n=1 hoặc n=0
2:
a: A=n(n+1)(n+2)
Vì n;n+1;n+2 là 3 số liên tiếp
nên A=n(n+1)(n+2) chia hết cho 3!=6
b: B=(2n-1)[(2n-1)^2-1]
=(2n-1)(2n-2)*2n
=4n(n-1)(2n-1)
Vì n;n-1 là hai số nguyên liên tiếp
nên n(n-1) chia hết cho 2
=>B chia hết cho 8
c: C=n^2+14n+49-n^2+10n-25=24n+24=24(n+1) chia hết cho 24

6n - 5 chia hết cho 2n-1
=» 3.2n-5 chia hết cho 2n-1
=» 3.2n-1+4 chia hết cho 2n - 1
=» 12 chia hết cho 2n-1
=» 2n-1 thuộc Ư (12)
Ư (12) = ( 1 ; 2 ; 3 ; 4 ; 6 ; 12 )
2n -1 E { 1 ; 2 ; 3 ; 4 ; 6 ; 12 }
2n E { 2 ; 3 ; 4 ; 5 ; 7 ; 13 }
n E {1 ; 1,5 ; 2 ; 2,5 ; 3,5 ; 6,5 }
mà n E Z
=> n E {1 ; 2 } thỏa mãn BT
4n-5 chia hết cho 2n-1
=» 3.2n-5 chia hết cho 2n-1
=» 3 . ( 2n - 1 ) - 4 chia hết cho 2n - 1
=» 4 chia hết cho 2n-1
=» 2n-1 thuộc Ư (4)
Ư (4) = ( 1;2;4)
=» 2n - 1 thuộc ( 1 ; 2 ; 4 )
=» 2n thuộc ( 2 ; 3 ; 5)
=» n = 1 thõa mãn BT
TÌM n thuộc Z để 2n2 – n + 2 chia hết 2n + 1.
Phép chia hết khi : 2n + 1 có giá trị là U(3) ={ ±1; ±3}
Vậy : n = 0, – 1, 1, – 2