Trong cùng 1 mặt phẳng toạ độ Oxy cho 3 điểm \(A\left(2;4\right);B\left(-3;-1\right);C\left(-2;1\right)\)
chứng minh 3 điểm A,B,C thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
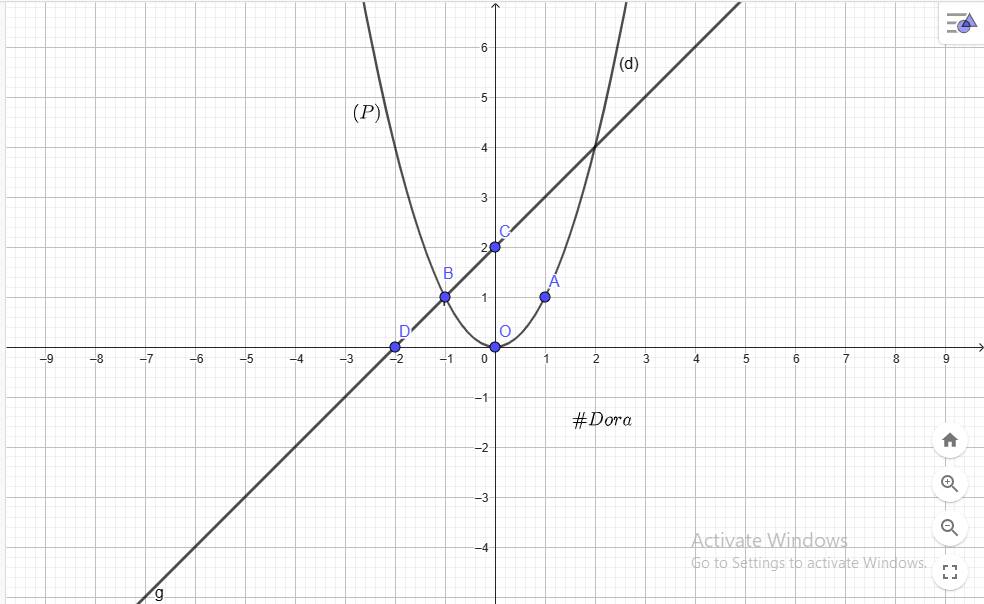
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến

Gọi \(M\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CM}=\left(x+5;y-1\right)\\\overrightarrow{AB}=\left(3;-7\right)\\\overrightarrow{AC}=\left(-4;-2\right)\end{matrix}\right.\) \(\Rightarrow2\overrightarrow{AB}-3\overrightarrow{AC}=\left(18;-8\right)\)
\(\overrightarrow{CM}=2\overrightarrow{AB}-3\overrightarrow{AC}\Leftrightarrow\left\{{}\begin{matrix}x+5=18\\y-1=-8\end{matrix}\right.\) \(\Rightarrow M\left(13;-7\right)\)

\(\overrightarrow{OA}=\left(3;1\right);\overrightarrow{OB}=\left(2;10\right)\)
\(\overrightarrow{OA}\cdot\overrightarrow{OB}=3\cdot2+1\cdot10=16\)

\(\left\{{}\begin{matrix}x=2+t\\y=1-3t\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6+3t\\y=1-3t\end{matrix}\right.\) \(\Rightarrow3x+y=7\Rightarrow3x+y-7=0\)
Vậy (d) có pt tổng quát là: \(3x+y-7=0\)
A và B nằm cùng phía đối với d khi và chỉ khi:
\(\left(3.1+2-7\right)\left(3.\left(-2\right)+m-7\right)>0\)
\(\Leftrightarrow-2\left(m-13\right)>0\)
\(\Rightarrow m< 13\)
Lời giải:
Gọi phương trình đường thẳng $AB$ là $y=ax+b$
Khi đó: \(\left\{\begin{matrix} 4=2a+b\\ -1=-3a+b\end{matrix}\right.\Rightarrow 5a=5\Rightarrow a=1\Rightarrow b=2\)
Vậy ptđt $AB$ có dạng $y=x+2$
Lại thấy: \(1\neq (-2)+2\) nên $C$ không thể thuộc đường thẳng $AB$
Suy ra $A,B,C$ không thẳng hàng. Bạn xem lại đề.
Gọi \(A\left(x_1;y_1\right);B\left(x_2;y_2\right);C\left(x_3;y_3\right)\)
Độ dài AB: \(AB=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)
\(=\sqrt{\left(2-\left(-3\right)\right)^2+\left(4-\left(-1\right)^2\right)}\) \(=5\sqrt{2}\) (đvđd)
Độ dài BC: \(BC=\sqrt{\left(\left(-3\right)-\left(-2\right)\right)^2+\left[\left(-1\right)-1\right]^2}\)
\(=\sqrt{\left(-1\right)^2+\left(-2\right)^2}\) \(=\sqrt{1+4}=\sqrt{5}\)(đvđd)
\(AC=\sqrt{\left(2-\left(-2\right)\right)^2+\left(4-1\right)^2}=5\)(đvđd)
\(\Rightarrow AB+BC\ne AC\)\(\Rightarrow A,B,C\) không thẳng hàng