Cho tứ diện S.ABC. Gọi O là điểm thuộc miền trong của tam giác ABC. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh SA, SC sao cho MN không song song với AC. Tìm tiết diện do (MNO) cắt tứ diện S.ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

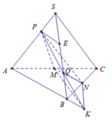
\(BC\) \(\subset\)\(\left(SBC\right)\)
Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):
\(N\)là điểm chung thứ nhất
Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)
\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)
Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)
\(K\)là điểm chung thứ 2.
Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)
Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)
Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)
Ta có N thuộc (OMN)
C thuộc đường thẳng BC
Mà N trùng với C => N là giao điểm của (OMN) và BC

Đáp án A
Gọi H là hình chiếu của S lên mặt đáy A B C suy ra S H ⊥ A B C thì H là trung điểm của AC.
Ta có:
S H = 9 − 2 = 7 ; K = P Q ∩ A B ; A B = A C = 2
Dựng P E / / A B ta có:
K B P E = Q B Q E = 1 ⇒ K B = P E = 1 3 A B = 2 3
S M N K = 1 2 d K ; M N . M N = 1 2 N B . M N = 1 2 d P ; A B C = 2 3 . S H = 2 3 7 ⇒ V P . M N K = 1 3 d P ; A B C . S M N K = 7 9
Lại có:
K Q K P = 1 2 ⇒ V Q . M N P V K . M N P = 1 2 ⇒ V Q . M N P = 1 2 V K . M N P = 7 18

Ta có
\(E\in MN\) mà \(MN\in\left(OMN\right)\Rightarrow E\in\left(OMN\right)\)
\(O\in\left(OMN\right)\)
\(\Rightarrow EO\in\left(OMN\right)\)
Ta có
\(E\in BD\) mà \(BD\in\left(BCD\right)\Rightarrow E\in\left(BCD\right)\)
\(O\in\left(BCD\right)\)
\(EO\in\left(BCD\right)\)
Trong (BCD) kéo dài EO cắt CD tại K
=> \(K\in\left(OMN\right);K\in CD\) => K chính là giao của CD với (OMN)

Đáp án C
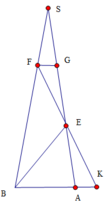
Ta có ∆ A B C vuông cân tại B nên M là tâm đường tròn ngoại tiếp. S M = S B = S C ⇒ S M ⊥ ( A B C )
F E ∩ A B = K , kẻ F G / / B A F H / / S M ⇒ F H ⊥ ( A B C ) ta có: F H = 2 3 S M = 2 3 S A 2 - A M 2 = 2 3 12 2 - 8 = 4 3 34
d t K M N = d t B N M K - d t B N K = 1 2 ( M N + B K ) . B N - 1 2 M N . B N = 1 2 . 2 . 2 = 2
∆ F G E = ∆ K A E ( C . G . C ) ⇒ F E = 1 2 F K
V F M N E V F M N K = F E F K = 1 2 ⇒ V F M N E = 1 2 V F M N K = 1 2 . 1 3 . F H . d t K M N = 1 6 . 4 3 34 . 2 = 4 34 9

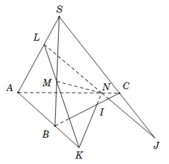
Ta có
+ M thuộc SB suy ra M là điểm chung của (LMN) và ( SBC) .
+ I là điểm chung của (LMN) và (SBC)
+ J là điểm chung của (LMN) và (SBC) .
Vậy M; I; J thẳng hàng vì cùng thuộc giao tuyến của (LMN) và (SBC).
Chọn B.

Tham khảo hình vẽ:
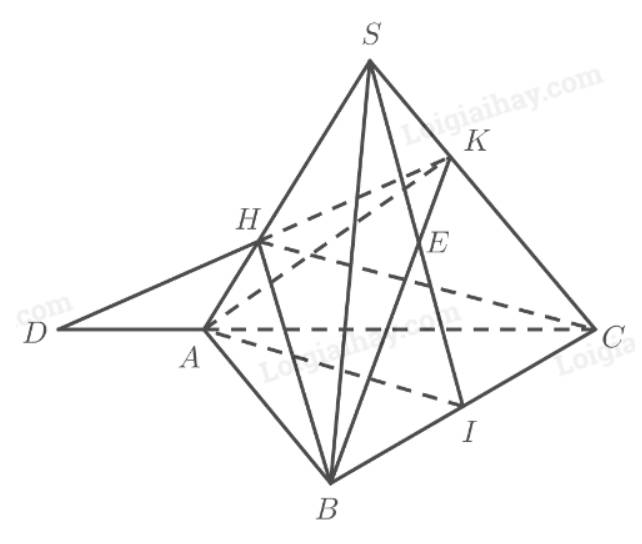
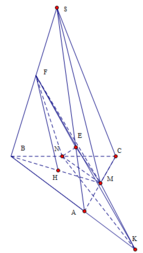
a) Gọi \(D = HK \cap AC\). Ta có:
\(\left. \begin{array}{l}D \in AC \subset \left( {ABC} \right)\\D \in HK\end{array} \right\} \Rightarrow M = HK \cap \left( {ABC} \right)\)
b) Gọi \(E = SI \cap BK\). Ta có:
\(\left. \begin{array}{l}E \in SI \subset \left( {SAI} \right)\\E \in BK \subset \left( {ABK} \right)\end{array} \right\} \Rightarrow E \in \left( {SAI} \right) \cap \left( {ABK} \right)\)
Mà \(A \in \left( {SAI} \right) \cap \left( {ABK} \right)\).
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\) là đường thẳng \(AE\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in \left( {SAI} \right)\\I \in BC \subset \left( {BCH} \right)\end{array} \right\} \Rightarrow I \in \left( {SAI} \right) \cap \left( {BCH} \right)\\\left. \begin{array}{l}H \in SA \subset \left( {SAI} \right)\\H \in \left( {BCH} \right)\end{array} \right\} \Rightarrow H \in \left( {SAI} \right) \cap \left( {BCH} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\) là đường thẳng \(HI\).