Cho a2+b2+4c2=2a-4b+4c-6.Xác định a;b;c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 12 2018
Đáp án D
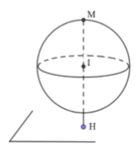
Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất
11 tháng 1 2018
Theo tôi nghĩ đề là như thế này :
Chứng minh :
\(\dfrac{1}{2a+b+c}+\dfrac{1}{a+2b+c}+\dfrac{1}{a+b+2c}\ge\dfrac{9}{4a+4b+4c}\)
Làm :
Áp dụng BĐT Cachy dạng phân thức, ta có :
\(\dfrac{1}{2a+b+c}+\dfrac{1}{a+2b+c}+\dfrac{1}{a+b+2c}\ge\dfrac{\left(1+1+1\right)^2}{2a+b+c+a+2b+c+a+b+2c}=\dfrac{9}{4a+4b+4c}\)
Dấu "=" xảy ra khi a = b = c .
=> ĐPCM
CM
23 tháng 10 2018
Ta có 
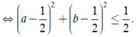
Ta có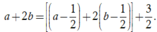 
Áp dụng bất đẳng thức Bunhiacopxky, ta có
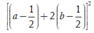
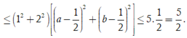
Do đó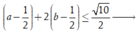 
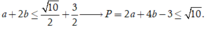
Dấu "x" xảy ra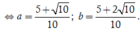 
Chọn C.
Ta thấy (1) là hình tròn tâm 
Ta có 
Xem đây là phương trình đường thẳng.
Để đường thẳng và hình tròn có điểm chung 
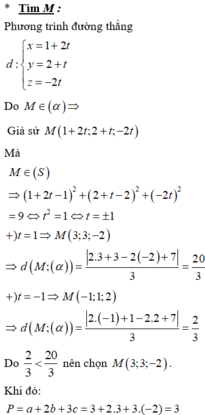
\(a^2+b^2+4c^2=2a-4b+4c-6\)
\(\Leftrightarrow a^2+2a+1+b^2+4b+4+4c^2-4c+1=0\)
\(\Leftrightarrow\left(a+1\right)^2+\left(b+2\right)^2+4\left(c^2-2.c.\dfrac{1}{2}+\dfrac{1}{4}\right)=0\)
\(\Leftrightarrow\left(a+1\right)^2+\left(b+2\right)^2+4\left(c-\dfrac{1}{2}\right)^2=0\)
Mà \(\left\{{}\begin{matrix}\left(a+1\right)^2\ge0\\\left(b+2\right)^2\ge0\\4\left(c-\dfrac{1}{2}\right)^2\ge0\end{matrix}\right.\Rightarrow\left(a+1\right)^2+\left(b+2\right)^2+4\left(c-\dfrac{1}{2}\right)^2\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}\left(a+1\right)^2=0\\\left(b+2\right)^2=0\\4\left(c-\dfrac{1}{2}\right)^2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=-1\\b=-2\\c=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(a=-1,b=-2,c=\dfrac{1}{2}\)