tìm GTNN
B = 3x2 + 6x - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LV
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Đề bài ko chính xác
Biểu thức này chỉ có GTLN, không có GTNN
CM
11 tháng 2 2019
Đặt và thực hiện phép tính ta có :
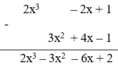
Vậy chọn đa thức thứ hai.
A
1
AH
Akai Haruma
Giáo viên
26 tháng 7 2021
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$\left(\frac{1}{a}+\frac{1}{b}\right)(a+b)\geq (1+1)^2$
$\Leftrightarrow B.3\geq 4$
$\Leftrightarrow B\geq \frac{4}{3}$
Vậy $B_{\min}=\frac{4}{3}$
Giá trị này đạt tại $a=b=\frac{3}{2}$
ND
1
13 tháng 11 2021
\(a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow x\left(x-1\right)+2\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
16 tháng 7 2021
Ta có tính chất `|P|>=P,|P|>=-P`
`=>{(|x-2|>=x-2),(|x-4|>=4-x):}`
`=>B>=x-2+4-x=2`
Dấu "=" xảy ra khi `{(x-2>=0),(x-4<=0):}`
`<=>{(x>=2),(x<=4):}`
`<=>2<=x<=4`
MH
25 tháng 8 2021
B=2(x^2+2.x.1/4 +1/16)^2 -57/8
=2.(x+1/4)^2 -57/8
MinB=-57/8 khi x=-1/4
25 tháng 8 2021
\(B=-14+2x^2+x=2\left(x^2+\dfrac{1}{2}x+\dfrac{1}{16}\right)-\dfrac{113}{8}=2\left(x+\dfrac{1}{4}\right)^2-\dfrac{113}{8}\ge-\dfrac{113}{8}\)\(ĐTXR\Leftrightarrow x=-\dfrac{1}{4}\)
3 tháng 10 2021
\(a,\Rightarrow x^3+9x^2+27x+27-9x^3-6x^2-x+8x^3+1-3x^2=54\\ \Rightarrow26x=26\Rightarrow x=1\\ b,\Rightarrow x^3-9x^2+27x-27-x^3+27+6x^2+12x+6+3x^2=-33\\ \Rightarrow39x=-39\Rightarrow x=-1\)
HQ
2
6 tháng 9 2023
a: =4(x^2-3/2x-5)
=4(x^2-2*x*3/4+9/16-89/16)
=4(x-3/4)^2-89/4>=-89/4
Dấu = xảy ra khi x=3/4
b: =3(x^2-8/3x+1)
=3(x^2-2*x*4/3+16/9-7/9)
=3(x-4/3)^2-7/3>=-7/3
Dấu = xảy ra khi x=4/3
AH
Akai Haruma
Giáo viên
6 tháng 9 2023
Lời giải:
a. $A=4x^2-6x-20=(2x)^2-2.2x.\frac{3}{2}+(\frac{3}{2})^2-\frac{89}{4}$
$=(2x-\frac{3}{2})^2-\frac{89}{4}$
Vì $(2x-\frac{3}{2})^2\geq 0$ với mọi $x$
$\Rightarrow A\geq 0-\frac{89}{4}=\frac{-89}{4}$
Vậy $A_{\min}=\frac{-89}{4}$. Giá trị này đạt tại $2x-\frac{3}{2}=0$
$\Leftrightarrow x=\frac{3}{4}$
b.
$B=3x^2-8x+1=3(x^2-\frac{8}{3}x)+1$
$=3[x^2-2.x.\frac{4}{3}+(\frac{4}{3})^2]-\frac{13}{3}$
$=3(x-\frac{4}{3})^2-\frac{13}{3}\geq 3.0-\frac{13}{3}=\frac{-13}{3}$
Vậy $B_{\min}=\frac{-13}{3}$. Giá trị này đạt tại $x-\frac{4}{3}=0$
$\Leftrightarrow x=\frac{4}{3}$
22 tháng 7 2021
Ta có : \(-4x^2+4x-5=-\left(4x^2-4x+5\right)=-\left(2x-1\right)^2-4\le-4\)
\(\Rightarrow B\ge\dfrac{15}{-4}\)
Dấu ''='' xảy ra khi x = 1/2
Vậy GTNN B là -15/4 khi x = 1/2
PT
1
CM
5 tháng 12 2017
9 x 2 - 6 x + 1 ≠ 0 ⇒ 3 x - 1 2 ≠ 0 ⇒ x ≠ 1 / 3 ta có x = - 8 ≠ 1/3
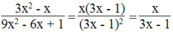
Thay x = - 8 vào biểu thức, ta có: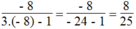 
= 3( x2 + 2x + 1) - 4
= 3(x + 1)2 - 4 \(\ge\) -4
Vậy Min B = -4 khi x + 1 = 0 => x = -1
B=3x^1+6x-1 > -1
=>Bmin=-1
GTNN của B=-1
tại x=....