các bạn giải giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(x=\dfrac{3}{4}-\dfrac{2}{4}=\dfrac{1}{4}\)
2: \(x=\dfrac{2}{11}+\dfrac{1}{5}=\dfrac{10+11}{55}=\dfrac{21}{55}\)
Có bạn nào giúp mình với! Bạn nào giải giúp mình sẽ theo dõi rồi tick! Cảm ơn các bạn rất nhiều!!!!!

Tớ giải lại phần a nhá :)) ?
Bài giải
a, Trong 2 tháng đầu năm , đội sản xuất làm được số sản phẩm là :
520 x 2 = 1040 ( sản phẩm )
Trong 3 tháng tiếp theo , đội sản xuất làm được số sản phẩm là :
600 x 3 = 1800 ( sản phẩm )
Trung bình mỗi tháng làm được số sản phẩm là :
( 1800 + 1040 ) : 5 = 568 ( sản phẩm )
Bài 34:
a) Trung bình mỗi tháng đội đó làm được số sản phẩm là:
$\frac{2\times 520+3\times 600}{2+3}=568$ (sản phẩm)
b)
Trung bình mỗi tháng đội đó cần làm số sản phẩm là:
$568+12=580$ (sản phẩm)
Tháng 6 đội đó cần làm số sản phẩm là:
$580\times 6-(2\times 520+3\times 600)=640$ (sản phẩm)

\(4x-2y-4x^2+4xy-y^2\)
\(=\left(4x-2y\right)-\left(4x^2-4xy+y^2\right)\)
\(=2\left(2x-y\right)-\left(2x-y\right)^2\)
\(=\left(2x-y\right)\left(2-2x+y\right)\)

280 - x.9 = 450
x.9 = 280 - 450
x.9 = -170
x= -170/9

1.
\(\Leftrightarrow1+2sin\dfrac{x}{2}cos\dfrac{x}{2}+\sqrt{3}cosx=3\)
\(\Leftrightarrow sinx+\sqrt{3}cosx=2\)
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow x-\dfrac{\pi}{6}=k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
2.
\(cos2x=-1\)
\(\Leftrightarrow2x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
3.
\(\left(2sinx-cosx\right)\left(1+cosx\right)=\left(1+cosx\right)\left(1-cosx\right)\)
\(\Leftrightarrow\left(1+cosx\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{6}\)
4.
\(1-cos2x-1-cos6x=0\)
\(\Leftrightarrow cos6x=-cos2x=cos\left(\pi-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}6x=\pi-2x+k2\pi\\6x=2x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Pt có 6 nghiệm trên khoảng đã cho

6.
\(sin3x+cos2x=1+sin3x-sinx\)
\(\Leftrightarrow cos2x=1-sinx\)
\(\Leftrightarrow1-2sin^2x=1-sinx\)
\(\Leftrightarrow2sin^2x-sinx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
7.
\(\sqrt{2}sinx-2\sqrt{2}cosx=2-2sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sinx\left(\sqrt{2}cosx+1\right)-2\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}sinx-2\right)\left(\sqrt{2}cosx+1\right)=0\)
\(\Leftrightarrow cosx=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow x=\pm\dfrac{3\pi}{4}+k2\pi\)
\(\left(\dfrac{3\pi}{4}\right).\left(-\dfrac{3\pi}{4}\right)=-\dfrac{9\pi^2}{16}\)
8.
\(2sinx.cosx+3cosx=0\)
\(\Leftrightarrow cosx\left(2sinx+3\right)=0\)
\(\Leftrightarrow cosx=0\)
\(\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{2}\) có 1 nghiệm trong khoảng đã cho
9.
\(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Đáp án D

Vì |2x-3| - |3x+2| = 0
Suy ra |2x-3|=|3x+2|
Ta có 2 trường hợp:
+)Trường hợp 1: Nếu 2x-3=3x+2
2x-3=3x+2
-3-2=3x-2x
-2=x
+)Trường hợp 2: Nếu 2x-3=-(3x+2)
2x-3=-(3x+2)
2x-3=-3x-2
2x+3x=3-2
5x=1
x=1/5
Vậy x thuộc {-1,1/5}
(2x - 3) - ( 3x + 2) = 0
tính trong ngoặc trước ngoài ngoặc sau
2x - 3 ko phải là 2 nhân âm 3.
2x = 2 nhân x
( 2x - 3) - ( 3x + 2) = 0 có nghĩa là 2x -3 = 3x + 2
còn đâu tự giải nhé


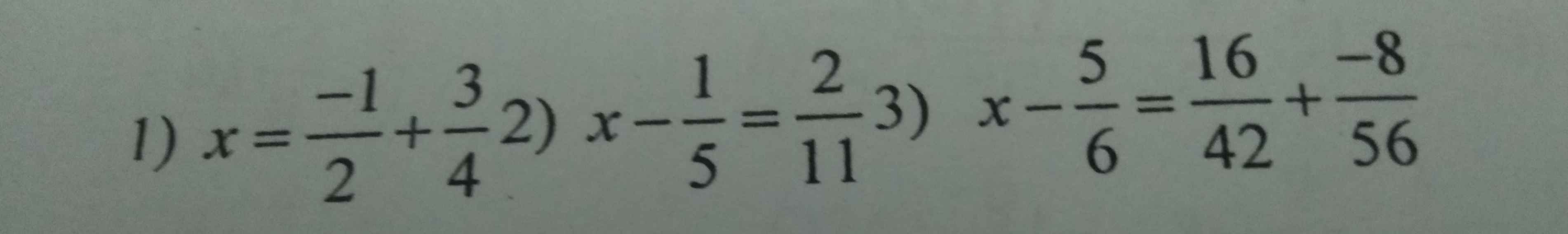





\(\hept{\begin{cases}x\left(x+y\right)-4=-x\\\left(x^2+2xy+y^2\right)-\frac{5}{x^2}=4\end{cases}\Leftrightarrow\hept{\begin{cases}\left(x+y\right)-\frac{4}{x}=-1\\\left(x^2+2xy+y^2\right)-\frac{5}{x^2}=4\end{cases}}}\)
Đặt \(\hept{\begin{cases}x+y=a\\\frac{1}{x}=b\end{cases}}\Rightarrow\hept{\begin{cases}a-4b=-1\\a^2-5b^2=4\end{cases}\Rightarrow a=4b-1}\)
\(\Rightarrow a^2-5b^2=4\Leftrightarrow\left(4a-1\right)^2-5b^2=4\Leftrightarrow\orbr{\begin{cases}b=1\Rightarrow a=3\\b=-\frac{3}{11}\Rightarrow a=-\frac{23}{11}\end{cases}}\)
vậy \(\orbr{\begin{cases}x=1,y=2\\x=-\frac{11}{3},y=\frac{5}{3}\end{cases}}\)