Giá trị lớn nhất,giá trị nho nhất của hàm số y=sinx-cosx lần lượt là: A.1;-1. B.\(\sqrt{2};-\sqrt{2}\). C.2;-2. D.3;-3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Vì ![]() nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình
nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình ![]() có nghiệm.
có nghiệm.
Sử dụng điều kiện có nghiệm của phương trình ![]() suy ra được
suy ra được ![]() vậy m = -1 và
vậy m = -1 và ![]()

Chọn B
Vì sinx-cosx+3>0 nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình (1-y)sinx+(y+1)cosx=(1+3y) có nghiệm.
Sử dụng điều kiện có nghiệm của phương trình A.sinx+B.cosx=C. Vậy m = -1 và M=1/7

Đáp án A
Ta có: y = cos x + 2 sin x + 3 2 cos x − sin x + 4
⇒ y 2 cos x − sin x + 4 = cos x + 2 sin x + 3
⇔ 2 + y sin x + 1 − 2 y cos x = 4 y − 3 1
PT (1) có nghiệm ⇔ 2 + y 2 + 1 − 2 y 2 ≥ 4 y − 3 2
⇔ 11 y 2 − 24 y + 4 ≤ 0 ⇔ 2 11 ≤ y ≤ 2
Suy ra M = 2 m = 2 11 ⇒ M . m = 4 11

Xét − sin x + 2 cos x + 4 = 0
Ta thấy − 1 2 + 2 2 < 4 2 nên phương trình vô nghiệm.
Do đó − sin x + 2 cos x + 4 ≠ 0 .
Như vậy, y = 2 sin x + cos x + 3 − sin x + 2 cos x + 4
⇔ y − sin x + 2 cos x + 4 = 2 sin x + cos x + 3
⇔ sin x 2 + y + cos x 1 − 2 y + 3 − 4 y = 0
Để phương trình có nghiệm thì 2 + y 2 + 1 − 2 y 2 ≥ 3 − 4 y 2
⇔ 5 y 2 + 5 ≥ 16 y 2 − 24 y + 9
⇔ 11 y 2 − 24 y + 4 ≤ 0
⇔ 2 11 ≤ y ≤ 2
Chọn đáp án D.

Đáp án C.
Ta có: f 2 x = 2 + sin x + cos x + 2 1 + sin x 1 + c o s x
= 2 + sin x + cos x + 2 1 + sin x + cos x + sin x cos x
Đặt t = sin x + cos x = 2 sin x + π 4 ⇒ t ∈ - 2 ; 2 .
Suy ra sin x cos x = t 2 - 1 2 ⇒ f 2 x = 2 + t + 2 1 + t + t 2 - 1 2 = 2 + t + 2 t 2 + 2 t + 1
⇒ f t = t + 2 + 2 t + 1 = t + 2 + 2 t + 1 k h i t ≥ - 1 t + 2 - 2 t + 1 k h i t < - 1 = 1 + 2 t + 2 + 2 k h i t ≥ - 1 1 - 2 t + 2 - 2 k h i t < - 1
Từ đó suy ra 1 ≤ f 2 x ≤ 4 + 2 2 ⇔ f x ≤ 4 + 2 2 ⇒ M - m = 4 + 2 2 - 1 .

\(ĐK:sinx-cosx\ne-2\)
\(< =>2y-1=sinx\left(1-y\right)+cosx\left(y+3\right)\)
Theo Bunhiacopxki:
\(\left[sinx\left(1-y\right)+cosx\left(y+3\right)\right]^2\)\(\le\left(sin^2x+cos^2x\right)\left[\left(1-y\right)^2+\left(y+3\right)^2\right]\)
\(< =>\left(2y-1\right)^2\le2y^2+4y+10\)
\(< =>2y^2-8y-9\le0\)
=> Bấm máy tìm Max, Min của y
(Sry máy tính của t bị ngáo không bấm ra)
\(\Rightarrow y.sinx-y.cosx+2y=sinx+3cosx+1\)
\(\Rightarrow\left(y-1\right)sinx-\left(y+3\right)cosx=1-2y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất
\(\Rightarrow\left(y-1\right)^2+\left(y+3\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2-8y-9\le0\)
\(\Rightarrow\dfrac{4-\sqrt{34}}{2}\le y\le\dfrac{4+\sqrt{34}}{2}\)
\(y_{max}=\dfrac{4+\sqrt{34}}{2}\) ; \(y_{min}=\dfrac{4-\sqrt{34}}{2}\)

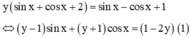

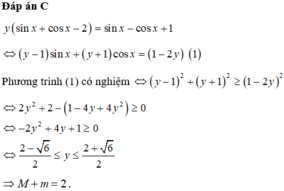
Lời giải:
Ta có \(y=\sin x-\cos x\Rightarrow y'=\cos x+\sin x=0\Leftrightarrow \cos x=-\sin x\)
Kết hợp với \(\cos^2x+\sin^2x=1\) suy ra \((\sin x,\cos x)=\left (\frac{1}{\sqrt{2}},\frac{-1}{\sqrt{2}}\right)\) hoặc \(\left (\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\)
Với \((\sin x,\cos x)=\left (\frac{1}{\sqrt{2}},\frac{-1}{\sqrt{2}}\right)\) thì \(y=\sqrt{2}\)
Với \((\sin x,\cos x)=\left (\frac{-1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\) thì \(y=-\sqrt{2}\)
Do đó \(y_{\max}=\sqrt{2};y_{\min}=-\sqrt{2}\)
Đáp án B
cách khác
đơn giản hóa vấn đề
\(A=sinx-cosx=sinx-sin\left(90^0-x\right)\)
\(A=2cos\left(\dfrac{\pi}{4}\right)sin\left(x-\dfrac{\pi}{4}\right)=\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)\)
\(-\sqrt{2}\le A\le\sqrt{2}\)