Cho hai góc kề bù AMB và BMC .
a, Tính số đo mỗi góc nếu hai góc này bằng nhau, nếu mỗi góc gấp đôi góc kia.
Từ điểm S nằm trên mỗi cạnh MA của góc AMB có thể kẻ được mấy đường thẳng vuông góc với cạnh MA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 6 2019
a) Sai vì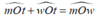 
chỉ đúng khi Ot là tia nằm giữa hai tia Om và Ow .
b) Đúng
c) Sai vì Hai góc có tổng bằng 180° là hai góc bù nhau.
d) Sai vì Hai góc kề bù là hai góc vừa kề nhau, vừa bù nhau.
e) Sai vì tổng số đo của hai góc nhọn có thể khác 90°
f) Sai
g) Sai vì nếu hai góc vuông không có cạnh chung thì không phải là hai góc kề bù.
h) Sai vì hai góc phụ nhau là hai góc có tổng số đo bằng 90°. Suy ra, biết số đo của một góc bằng 45° thì số đo của góc còn lại cũng bằng 45°.
i) Sai vì hai góc bù nhau là hai góc có tổng số đo bằng 180°. Suy ra, biết số đo của một góc bằng 45° thì số đo góc còn lại bằng 135° .
Vậy trong bài này chỉ có câu b là đúng, các câu còn lại là sai.
25 tháng 9 2020
( Hình ảnh chỉ mang t/c mih họa)
Ta có: \(\widehat{mOy}=\frac{1}{2}\widehat{xOy}\left(gt\right)\)
\(\widehat{yOn}=\frac{1}{2}\widehat{yOz}\left(gt\right)\)
Vì Oy nằm giữa 2 tia Om, On nên
\(\widehat{mOn}=\widehat{mOy}+\widehat{yOn}\)
\(=\frac{1}{2}\widehat{xOy}+\frac{1}{2}\widehat{yOz}\)
\(=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)\)\(=\frac{1}{2}.180^o=90^o\)( kề bù)
\(\Rightarrow Om\perp On\)(đpcm)
CM
25 tháng 1 2019
Trên hình 2.8a) có A H ⊥ O x , A K ⊥ O y nên các góc có cạnh tương ứng vuông góc là: góc HAK và góc xOy; góc HAt và góc xOy.
Trên hình 2.8b) có A B ⊥ A C ; A H ⊥ B C và nên các góc có cạnh tương ứng vuông góc là: góc BAH và góc C; góc CAH và góc B.
a) (+) Nếu hai góc kề bù AMB và BMC bằng nhau thì ta có:
\(\widehat{AMB}=\widehat{BMC}=\dfrac{180^o}{2}=90^o\)
Vậy khi hai góc bằng nhau thì ta có: \(\widehat{AMB}=\widehat{BMC}=90^o\)
(+) Nếu giả sử góc AMB lớn gấp hai lần góc BMC thì ta có:
\(1\widehat{AMB}=2\widehat{BMC}\left(\widehat{AMB}+\widehat{BMC}=180^o\right)\)
\(\Rightarrow\widehat{AMB}=180:3.2=120^o\)
\(\Rightarrow\widehat{BMC}=180^o-120^o=60^o\)
Vậy khi góc AMB lớn gấp đôi góc BMC thì \(\widehat{AMB}=120^o\)
\(\widehat{BMC}=60^o\)
Nếu điều giả sử ngược lại thì kết quả cũng ngược lại
b) 2 đường thẳng nhé