Gọi G,G' lần lượt là trọng tâm của tam giác ABC và A'B'C(các đường thẳng AA',BB',CC' không cắt nhau).Chứng minh GG'=1/3(AA'+BB'+CC')
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
5 tháng 10 2017
Chứng minh:
\(\widehat{IDM}=\widehat{IDN}\) ( vì \(DI\) là tia pân giác của \(\widehat{MDN}\)) (1)
\(\widehat{IDM}=\widehat{EDK}\) ( hai góc đối đỉnh )
Từ (1) và (2) suy ra : \(\widehat{EDK}=\widehat{IDN}\left(đpcm\right)\)
Chúc bạn học tốt!
5 tháng 10 2017
Ta có: Chứng minh:IDM=IDN (Vì DI là tia phân giác của MDN ) (1)
Ta có: IDM=EDK (Vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra: EDK=IDN (điều phải chứng minh)
CM
4 tháng 8 2018
Chọn D
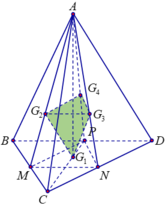
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay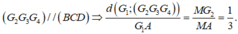 
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
G(-2) = (-2)2 – 4 = 4 – 4 = 0;
G(1) = 12 – 4 = 1 – 4 = -3;
G(0) = 02 – 4 = 0 – 4 = -4;
G(1) = 12 – 4 = 1- 4 = -3;
G(2) = 22 – 4 = 4 – 4 = 0
4 tháng 12 2021
a: Xét ΔMNP có
Q là trung điểm của MN
K là trung điểm của NP
Do đó: QK là đường trung bình của ΔMNP
Suy ra: QK//MP
hay MQKP là hình thang vuông
Y
27 tháng 5 2019
a) \(\left\{{}\begin{matrix}\widehat{OBH}+\widehat{BOH}=90^o\\\widehat{OCK}+\widehat{COK}=90^o\end{matrix}\right.\)
\(\Rightarrow\widehat{BOH}=\widehat{COK}\)
+ ΔBOH vuông tại H, đg trung tuyến HE
=> \(HE=\frac{1}{2}BO\) ( theo tính chất đg trung tuyến trong Δ vuông )
=> HE = BE = OE
=> ΔOHE cân tại E
\(\Rightarrow\widehat{OEH}=180^o-2\cdot\widehat{EOH}\) \(=180^o-2\cdot\widehat{FOK}\)
+ Tương tự ta cm đc :
ΔFOK cân tại F
\(\Rightarrow\widehat{OFK}=180^o-2\cdot\widehat{FOK}\)
\(\Rightarrow\widehat{OEH}=\widehat{OFK}\)
b) + EM là đg trung bình của ΔBOC
\(\Rightarrow\left\{{}\begin{matrix}EM=\frac{1}{2}CO\\EM//OC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}EM=OF=KF\\\widehat{OEM}+\widehat{EOF}=180^o\end{matrix}\right.\) (1)
+ Tương tự : \(\left\{{}\begin{matrix}FM=OE=EH\\\widehat{OFM}+\widehat{EOF}=180^o\end{matrix}\right.\) (2)
+ Từ (1) và (2) suy ra : \(\left\{{}\begin{matrix}KF=ME\\HE=MF\\\widehat{OEM}=\widehat{OFM}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}KF=ME\\HE=MF\\\widehat{HEM}=\widehat{KFM}\left(do\widehat{OEH}=\widehat{OFK}\right)\end{matrix}\right.\)
ΔEMH = ΔFKM ( c.g.c )
=> MH = MK
27 tháng 5 2019
Bài 1a :
ˆBOH=ˆKOCBOH^=KOC^
Lại có : HE=EO=BE và KF=FO=OC => 2.ˆKOF=2ˆHOE=>ˆOEH=ˆOFK
Bài 1b :
Do FM và DM là đường trung bình tam giác BOC => DM=OF=KF ; FM=OD=HD
ˆHDO=ˆKFOHDO^=KFO^ ; do FM // OD ; OF // DM => DMFO là hình bình hành
=>ˆODM=ˆOFM=>ˆHDM=ˆKFM=>△HDM=△MFK(c.c.c)=>HM=MKODM^=OFM^=>HDM^=KFM^=>△HDM=△MFK(c.c.c)=>HM=MK
13 tháng 5 2019
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
CM
17 tháng 4 2019
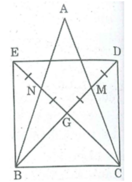
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ∆ ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN, có: BC cạnh chung
∠ (BCM) = ∠ (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ∆ BCM = ∆ CBN (c.g.c)
⇒ ∠ (MBC) = ∠ (NCB) ⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.