Question

[Perfect Blue]

mn giúp t nhé , tks

Answer 1

[Akai Haruma]

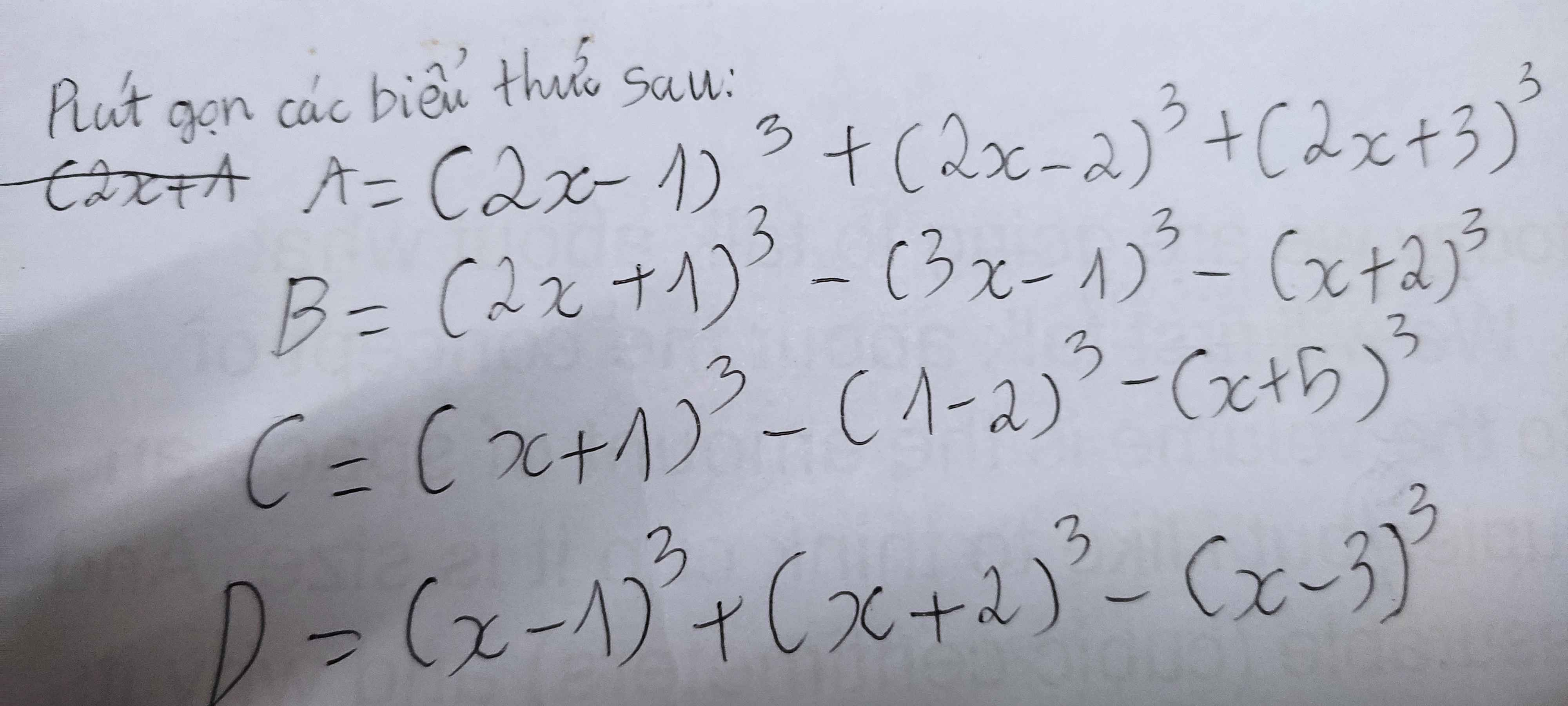
Lời giải:

Áp dụng BĐT AM-GM:

\((2a+b+c)^2=a^2+(a+b+c)^2+2a(a+b+c)=a^2+\frac{(a+b+c)^2}{9}+\frac{8(a+b+c)^2}{9}+2a(a+b+c)\)

\(\geq \frac{2a(a+b+c)}{3}+\frac{8(a+b+c)^2}{9}+2a(a+b+c)=\frac{8(a+b+c)^2}{9}+\frac{8a(a+b+c)}{3}\)

Suy ra \(\frac{1}{(2a+b+c)^2}\leq \frac{9}{8(a+b+c)(4a+b+c)}\Rightarrow \sum \frac{1}{(2a+b+c)^2}\leq \frac{9}{8(a+b+c)}\sum \frac{1}{4a+b+c}\)

Áp dụng BĐT Cauchy-Schwarz:

\(\frac{1}{4a+b+c}\leq \frac{1}{36}\left (\frac{1}{a}+\frac{1}{a}+\frac{1}{a}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{1}{36}\left (\frac{4}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

\(\Rightarrow \sum \frac{1}{4a+b+c}\leq \frac{1}{6}\left (\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

Do đó \(\sum \frac{1}{(2a+b+c)^2}\leq \frac{9}{8(a+b+c)}\sum \frac{1}{4a+b+c}\leq \frac{9}{8(a+b+c)}.\frac{1}{6}\left (\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{9}{8}.\frac{1}{6}=\frac{3}{16}\)

Ta có đpcm

Dấu bằng xảy ra khi \(a=b=c=1\)