Cho X={1;2;3;4;5;6;7;8;9}. Có bao nhiêu số tự nhiên gồm 6 chữ số được lấy từ X mà tổng các chữ số là một số lẻ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1,
a, x + 1 ⋮ 16
=> x + 1 thuộc B(16)
=> x + 1 thuộc {0;; 16; 32; 64;....}
=> x thuộc {-1; 15; 31; 63; ...}
các phần còn lại làm tương tự

2: \(\Leftrightarrow x+2\in\left\{1;-1\right\}\)
hay \(x\in\left\{-1;-3\right\}\)

a; \(x\) + 6 ⋮ \(x\) + 1 (\(x\) ≠ - 1)
\(x\) + 1 + 5 ⋮ \(x\) + 1
\(x\) + 1 \(\in\) Ư(5) = {-5; -1; 1; 5}
\(x\) \(\in\) {-6; -2; 0; 4}
\(x\) + 6 ⋮ \(x\) + (-1) (\(x\) ≠ 1)
\(x\) + - 1 + 7 ⋮ \(x\) - 1
7 ⋮ \(x\) - 1
\(x\) - 1 \(\in\) Ư(7) = {-7; -1; 1; 7}
\(x\) \(\in\) {-6; 0; 2; 8}
b; \(x\) + 6 ⋮ \(x\) - 2 (đk \(x\) ≠ 2)
\(x\) - 2 + 8 ⋮ \(x\) - 2
8 ⋮ \(x\) - 2
\(x\) - 2 \(\in\) Ư(8) = {-8; -4; -2; -1; 1; 2; 4; 8}
\(x\) \(\in\) {-6; -2; 0; 1; 3; 4; 10}
\(x\) + 6 ⋮ \(x\) + (-2)
\(x\) + 6 ⋮ \(x\) - 2
giống với ý trên

a) (x + 6) - x chia hết cho x => 6 chia hết cho x hay xÎƯ(6) = {-6; -3; -2; -l; l; 2; 3; 6}.
b) ( x +9) - (x + l) chia hết cho (x + l) =>8 chia hết cho (x + l)
=> x + 1 ÎƯ (8) = { - 8; -4; -2; -1; 1; 2; 4; 8}.
Từ đó tìm được x Î {- 9; - 5; - 3; - 2; 0; 1; 3; 7}.
c) (2 + l) -2 (x - l) chia hết cho (x - l) => 3 chia hết cho (x - l)
=> x - 1Î Ư (3) = {- 3; -1; 1; 3}. Từ đó tìm được x Î{ - 2; 0; 2; 4}.

a, \(x\) + 6 ⋮ \(x\) đkxđ \(x\) \(\ne\) 0
⇔ 6 ⋮ \(x\)
\(x\) \(\in\) {1; 2; 3; 6}
b, \(x\) + 9 \(⋮\) \(x\) + 1 đkxđ \(x\) \(\ne\) -1
\(x\) + 1 + 8 ⋮ \(x\) + 1
8 \(⋮\) \(x\) + 1
\(x\) + 1 \(\in\) Ư(8) = { 1; 2; 4; 8}
\(x\) \(\in\) { 0; 1; 3; 7}
c, 2\(x\) + 1 ⋮ \(x\) - 1 đkxđ \(x\) \(\ne\) 1
2\(x\) - 2 + 3 ⋮ \(x\) -1
2.(\(x\) - 1) + 3 \(⋮\) \(x\) - 1
\(x\) - 1 \(\in\)Ư(3) = { 1; 3}
\(x\) \(\in\) { 2; 4}

a) Xem lại đề!
b) Ta có:
x + 9 = x + 1 + 8
Để (x + 9) ⋮ (x + 1) thì 8 ⋮ (x + 1)
⇒ x + 1 ∈ Ư(8) = {-8; -4; -2; -1; 1; 2; 4; 8}
⇒ x ∈ {-9; -5; -3; -2; 0; 1; 3; 7}
Mà x ∈ ℕ
⇒ x ∈ {0; 1; 3; 7}
c) Ta có:
2x + 1 = 2x - 2 + 3 = 2(x - 1) + 3
Để (2x + 1) ⋮ (x - 1) thì 3 ⋮ (x - 1)
⇒ x - 1 ∈ Ư{3} = {-3; -1; 1; 3}
⇒ x ∈ {-2; 0; 2; 4}
Mà x ∈ ℕ
⇒ x ∈ {0; 2; 4}
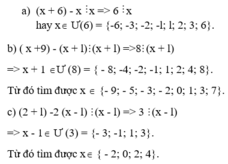
Đề có yêu cầu gì về các chữ số phân biệt hay không nhỉ?