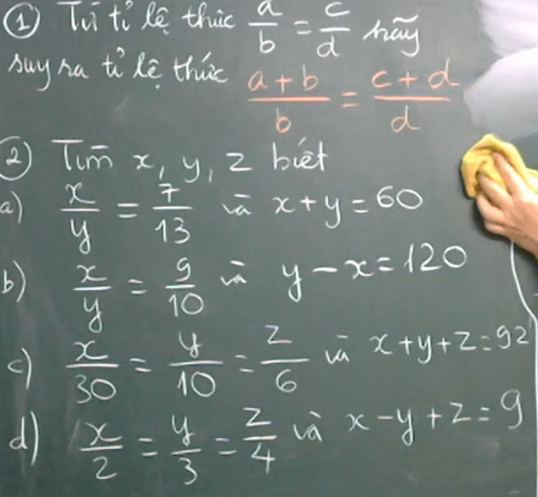
Làm hết hộ em nha!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2021
a) Ta có:
\(\dfrac{x}{5}=\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\\ \Rightarrow\left\{{}\begin{matrix}x=9\cdot5=45\\y=9\cdot3=27\\z=9\cdot4=36\end{matrix}\right.\)
Vậy x = 45; y = 27; z = 36.
b) Ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}\)\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{15}\)
\(\dfrac{y}{3}=\dfrac{z}{5}\)\(\Rightarrow\dfrac{y}{15}=\dfrac{z}{25}\)
suy ra, \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\\
\Rightarrow\left\{{}\begin{matrix}x=-2\cdot6=-12\\y=-2\cdot15=-30\\z=-2\cdot25=-50\end{matrix}\right.\)
Vậy x = -12; y = -30; z = -50.
c) Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=4\\ \Rightarrow\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=8\end{matrix}\right.\\\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\\\left\{{}\begin{matrix}x=-6\\y=-8\end{matrix}\right.\end{matrix}\right.\)
Vậy (x; y) \(\in\left\{\left(6;8\right);\left(-6;8\right);\left(6;-8\right);\left(-6;-8\right)\right\}\)
d), Ta có:
\(2x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\Rightarrow\dfrac{x}{21}=\dfrac{y}{14}\\ 5y=7z\Rightarrow\dfrac{y}{7}=\dfrac{z}{5}\Rightarrow\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\\ \Rightarrow\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}=\dfrac{3x-7y+5z}{63-98+50}=\dfrac{30}{15}=2\\
\Rightarrow\left\{{}\begin{matrix}x=2\cdot21=42\\y=2\cdot14=28\\z=2\cdot10=20\end{matrix}\right.\)
Vậy x = 42; y = 28; z = 20.
25 tháng 8 2021
a: Ta có: \(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{4}\)
nên \(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{10}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2x+y-z}{10+3-4}=\dfrac{81}{9}=9\)
Do đó: x=45; y=27; z=36
b: Ta có: \(\dfrac{x}{2}=\dfrac{y}{5}\)
nên \(\dfrac{x}{6}=\dfrac{y}{15}\left(1\right)\)
Ta có: \(\dfrac{y}{3}=\dfrac{z}{5}\)
nên \(\dfrac{y}{15}=\dfrac{z}{25}\left(2\right)\)
Từ (1), (2) suy ra \(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}\)
mà x+y+z=-92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{15}=\dfrac{z}{25}=\dfrac{x+y+z}{6+15+25}=-\dfrac{92}{46}=-2\)
Do đó: x=-12; y=-30; z=-50
c: Ta có: \(\dfrac{x^2}{9}=\dfrac{y^2}{16}\)
mà \(x^2+y^2=100\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
Do đó: \(\left\{{}\begin{matrix}x^2=36\\y^2=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{6;-6\right\}\\y\in\left\{8;-8\right\}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
a.
$4x=3y\Rightarrow 20x=15y$
$5y=3z\Rightarrow 15y=9z$
$\Rightarrow 20x=15y=9z=t$
$\Rightarrow x=\frac{t}{20}; y=\frac{t}{15}; z=\frac{t}{9}$
Khi đó:
$2x-3y+z=\frac{2t}{20}-\frac{3t}{15}+\frac{t}{9}=5$
$\frac{t}{90}=6$
$t=540$
$x=\frac{540}{20}=27; y=\frac{540}{15}=36;z=\frac{540}{9}=60$
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
b. Đặt $5x=8y=3z=t$
$\Rightarrow x=\frac{t}{5}; y=\frac{t}{8}; z=\frac{t}{3}$
Khi đó:
$x-2y+z=34$
$\frac{t}{5}-\frac{2t}{8}+\frac{t}{3}=34$
$\frac{17}{60}t=34$
$t=120$
$x=\frac{120}{5}=24; y=\frac{120}{8}=15; z=\frac{120}{3}=40$
c.
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$
Khi đó:
$x^2+3y^2-2z^2=-16$
$(2t)^2+3(3t)^2-2(4t)^2=-16$
$-t^2=-16$
$t^2=16$
$t=\pm 4$
Khi $t=4$ thì $x=2.4=8; y=3.4=12; z=4.4=16$
Khi $t=-4$ thì $x=-8; y=-12; z=-16$
17 tháng 12 2022
Cuối tuần vừa rồi em được mẹ đưa đi nhổ răng sâu. Ở đó, em được gặp bác sĩ Lan - người giúp em cảm nhận được tấm lòng ấm áp của một y sĩ.
Bác sĩ Lan trông còn khá trẻ, khoảng hơn 25 tuổi mà thôi. Cô ấy có vóc dáng đầy đặn, nhưng vẫn rất gọn gàng và nhanh nhẹn. Để đảm bảo an toàn, cô Lan mặc bộ đồng phục trắng tinh của bệnh viện và đeo khẩu trang che kín cả khuôn mặt. Ngay cả mái tóc cũng được búi gọn trong chiếc mũ. Tuy không thể nhìn thấy khuôn mặt của cô, nhưng lắng nghe giọng nói dịu dàng, ấm áp em vẫn có thể chắc chắn rằng cô Lan rất xinh đẹp.Sau khi hỏi về một số thông tin cơ bản, em bắt đầu được bác sĩ Lan nhổ răng. Vì chân răng đã lung lay nên công việc sẽ khá đơn giản. Tuy nhiên em vẫn rất lo lắng, nên tay chân cứ run lên. Thấy thế, bác sĩ đã dịu dàng cầm tay em, nói những lời thủ thỉ dịu dàng. Cô ấy còn kể một vài câu chuyện cười để em quên đi nỗi sơn. Cuối cùng, với động tác dịu nhẹ của bác sĩ, em đã nhổ được chiếc răng sâu mà chẳng đau tí nào. Trước lúc về, bác còn cẩn thận dặn dò em những điều cần lưu ý khi mới nhổ răng nữa. Thật là tận tâm.
Em quý bác sĩ Lan lắm. Em mong rằng không chỉ cô ấy, mà còn tất cả các y bác sĩ khác luôn luôn khỏe mạnh để có thể khám chữa cho thật nhiều người.
17 tháng 12 2022
Có gợi ý nha (Bạn nào học lớp 5 có thể mở Sách Luyện tập Tiếng Việt Tập 1 tuần 16 tiết 3 trang 94-95-96) các bạn
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
Câu 9 cần bs điều kiện $x,y,z\neq 0$
$\frac{x}{3}=\frac{y}{4}\Rightarrow \frac{x}{15}=\frac{y}{20}$
$\frac{y}{5}=\frac{z}{6}\Rightarrow \frac{y}{20}=\frac{z}{24}$
$\Rightarrow \frac{x}{15}=\frac{y}{20}=\frac{z}{24}$ và đặt $=t$ (đk: $t\neq 0$)
$\Rightarrow x=15t; y=20t; z=24t$
Khi đó:
$M=\frac{2.15t+3.20t+4.24t}{3.15t+4.20t+5.24t}=\frac{186t}{245t}=\frac{186}{245}$
Đáp án B.
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
Câu 10:
Giả sử số $A$ được chia thành 3 phần $a,b,c$ sao cho
$a:b:c=\frac{2}{5}: \frac{3}{4}: \frac{1}{6}$
Đặt $a=\frac{2}{5}t; b=\frac{3}{4}t; c=\frac{1}{6}t$
$A=a+b+c=\frac{2}{5}t+\frac{3}{4}t+\frac{1}{6}t=\frac{79}{60}t$
Có:
$a^2+b^2+c^2=(\frac{2}{5}t)^2+(\frac{3}{4}t)^2+(\frac{1}{6}t)^2=24309$
$t^2=32400$
$t=\pm 180$
$\Rightarrow A=\frac{79}{60}t=\frac{79}{60}\pm 180=\pm 237$
Đáp án D.
Bài 2:
a) \(\dfrac{x}{y}=\dfrac{7}{13}\Rightarrow\dfrac{x}{7}=\dfrac{y}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{60}{20}=3\)
\(\dfrac{x}{7}=3\Rightarrow x=21\\ \dfrac{y}{13}=3\Rightarrow y=39\)
b) \(\dfrac{x}{y}=\dfrac{9}{10}\Rightarrow\dfrac{x}{9}=\dfrac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{9}=\dfrac{y}{10}=\dfrac{y-x}{10-9}=120\)
\(\dfrac{x}{9}=120\Rightarrow x=1080\\ \dfrac{y}{10}=120\Rightarrow y=1200\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y+z}{30+10+6}=\dfrac{92}{46}=2\)
\(\dfrac{x}{30}=2\Rightarrow x=60\\ \dfrac{y}{10}=2\Rightarrow y=20\\ \dfrac{z}{6}=2\Rightarrow z=12\)
d)Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y+z}{2-3+4}=\dfrac{9}{3}=3\)
\(\dfrac{x}{2}=3\Rightarrow x=6\\ \dfrac{y}{3}=3\Rightarrow y=9\\ \dfrac{z}{4}=3\Rightarrow z=12\)
Bài 1:
\(\dfrac{a+b}{b}=\dfrac{a}{b}+1\)
\(\dfrac{c+d}{d}=\dfrac{c}{d}+1\)
Mà \(\dfrac{a}{b}=\dfrac{c}{d};1=1\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)