Tìm nghiệm nguyên của phương trình
1. x4 - 5x2y2 + 4y4 = 3
2. x3 + y3 + z3 - 3xyz = 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 9 2021
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
CM
8 tháng 8 2019
a) 16(12 t 2 +1).
b) Gợi ý x 3 + y 3 = ( x + y ) 3 - 3xy(x + y)
(x + y - z)( x 2 + y 2 + z 2 - xy + xz + yz).
CM
12 tháng 10 2017
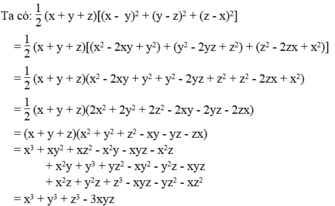
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
26 tháng 1 2018
+, Nếu x = 0 => ko tồn tại y thuộc Z
+, Nếu x khác 0 => x^2 >= 1 => x^2-1 >= 0
Có : y^3 = x^3+2x^2+3x+2 > x^3 ( vì 2x^2+3x+2 > 0 )
Lại có : y^3 = (x^3+3x^3+3x+1)-(x^2-1) = (x+1)^3 - (x^2-1) < = (x+1)^3
=> x^3 < y^3 < = (x+1)^3
=> y^3 = (x+1)^3
=> x^2-1 = 0
=> x=-1 hoặc x=1
+, Với x=-1 thì y = 0
+, Với x=1 thì y = 2
Vậy .............
Tk mk nha
BM
26 tháng 1 2018
Ta có: \(x^3+2x^2+3x+2=y^3\) (1)
Xét \(2x^2+3x+2=2\left(x^2+\frac{3}{2}x\right)+2=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+2-2.\frac{9}{16}\)
\(=2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\) Vì \(\left(x+\frac{3}{4}\right)^2\ge0\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{7}{8}\ge\frac{7}{8}>0\)
\(\Rightarrow y^3>x^3\Rightarrow y^3\ge\left(x+1\right)^3\)
\(\Rightarrow x^3+2x^2+3x+2\ge\left(x+1\right)^3\) \(\Rightarrow x^3+2x^2+3x+2\ge x^3+3x^2+3x+1\)
\(\Rightarrow x^3+3x^2+3x+1-x^3-2x^2-3x-2\le0\)
\(\Rightarrow x^2-1\le0\Rightarrow x^2\le1\) Vì \(x\in Z\Rightarrow\orbr{\begin{cases}x^2=1\\x^2=0\end{cases}}\)
+ TH1: x2 = 0 => x =0 Thay vào pt (1) ta được y3 = 2 (loại) vì y nguyên
+ TH2 : x2 = 1 => \(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Thay x=1 vào pt (1) ta đc: 1+2+3+2 = 8 = y3 => y = 2
Thay x= -1 vào pt (1) ta đc: -1 + 2 -3 +2 = 0 =y3 => y = 0
Vậy cặp (x;y) là (1;2) ; (-1;0).
DV
2
XO
1 tháng 1 2022
x3 + y3 + 1 = 6xy
<=> (x + y)3 - 3xy(x + y) + 1 = 6xy
<=> (x + y)3 + 8 - 3xy(x + y + 2) = 7
<=> (x + y + 2)(x2 - xy + y2 + 2x + 2y + 4) = 7
Đến đây bạn tự giải tiếp
DV
0
16 tháng 5 2023
a: =(x+y)^3+z^3-3xy(x+y)-3xyz
=(x+y+z)(x^2+2xy+y^2-xz-yz+z^2)-3xy(x+y+z)
=(x+y+z)(x^2+y^2+z^2-xy-xz-yz)
b: a+b+c<>0
A=(a+b+c)^3-a^3-b^3-c^3/a+b+c
=(a+b+c)(a^2+b^2+c^2-ab-ac-bc)/(a+b+c)
=a^2+b^2+c^2-ab-ac-bc
=1/2[a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2]
=1/2[(a-b)^2+(b-c)^2+(a-c)^2]>=0
NA
1
26 tháng 2 2020
Ta rút gọn tử thức trc: \(x^3+y^3+z^3-3xyz=x^3+y^3+z^3+x^2y-x^2y+xy^2-xy^2+y^2z-y^2z+yz^2-yz^2+x^2z-x^2z+xz^2-xz^2-xyz-xyz-xyz=x^2\left(x+y+z\right)+y^2\left(x+y+z\right)+z^2\left(x+y+z\right)-x\left(x+y+z\right)-yz\left(x+y+z\right)-xz\left(x+y+z\right)=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)=\frac{1}{2}\left(x+y+z\right)\left(x^2-2xy+y^2+y^2-2yz+z^2+z^2-2xz+x^2\right)=\frac{1}{2}\left(x+y+z\right)\left(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right)\)tới đây rút gọn đc rồi chứ