4x+2 +2 . 4x= 288
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
LQ
1
29 tháng 8 2021
\(288-\left(88+5^4\right)-\left(4x^4-200\right)=416\)
\(\Leftrightarrow288-88-625-4x^4+200=416\)
\(\Leftrightarrow-4x^4-225=416\)
\(\Leftrightarrow-4x^4=641\)(vô lý)
LQ
2
29 tháng 8 2021
\(288-\left(88+5^4\right)-\left(4x^4-200\right)=416\)
\(\Leftrightarrow288-88-625-4x^4+200=416\)
\(\Leftrightarrow-4x^4-225=416\)
\(\Leftrightarrow-4x^4=641\)(vô lý)
KK
29 tháng 8 2021
288 - (88 + 54) - (4x4 - 200) = 416
<=> 288 - 88 - 625 - 4x4 + 200 = 416
<=> 288 - 88 - 625 - 416 + 200 = 4x4
<=> -641 = 4x4
<=> x4 = -160,25
<=> x = \(-\sqrt[4]{160,25}\) = -3,557947288 \(\approx\) -3,56
26 tháng 9 2021
Bài 3:
a: Ta có: 60-3(x-2)=51
\(\Leftrightarrow x-2=3\)
hay x=5
b: Ta có: \(4x-20=25:2^2\)
\(\Leftrightarrow4x=\dfrac{25}{4}+20=\dfrac{105}{4}\)
hay \(x=\dfrac{105}{16}\)
c: Ta có: \(8\cdot6+288:\left(x-3\right)^2=50\)
\(\Leftrightarrow288:\left(x-3\right)^2=50-48=2\)
\(\Leftrightarrow\left(x-3\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=12\\x-3=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=-9\end{matrix}\right.\)
4 tháng 10 2021
ta có 4 x 3 y 2 – 8 x 2 y 3 = 4 x 2 y 2 . x – 4 x 2 y 2 . 2 y = 4 x 2 y 2 ( x – 2 y )
Vậy 4x3y2 – 8x2y3 = 4x2y2(x – 2y)
Đáp án cần chọn là: C
bấm đúng cho mik đi
DQ
2
11 tháng 7 2021
Ta có: \(\sqrt{4x^2-4x+1}-\sqrt{4x^2+4x+1}\)
\(=\sqrt{\left(2x-1\right)^2}-\sqrt{\left(2x+1\right)^2}\)
\(=\left|2x-1\right|-\left|2x+1\right|\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
28 tháng 6 2023
(4x2)8: (4x2)4: (4x2)2= (4x2)8-4-2= (4x2)2=16x4
TA
2
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 8 2023
\(4x^2-4x+1=\left(2x\right)^2-2.2x.1+1^2=\left(2x-1\right)^2\\ ---\\ 4x^2-4x-3\\ =4x^2-4x+1-4\\ =\left(2x-1\right)^2-2^2=\left(2x-1-2\right)\left(2x-1+2\right)\\ =\left(2x-3\right)\left(2x+1\right)\)
11 tháng 8 2023
1: =(2x)^2-2*2x*1+1^2
=(2x-1)^2
2: =4x^2-6x+2x-3
=2x(2x-3)+(2x-3)
=(2x-3)(2x+1)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
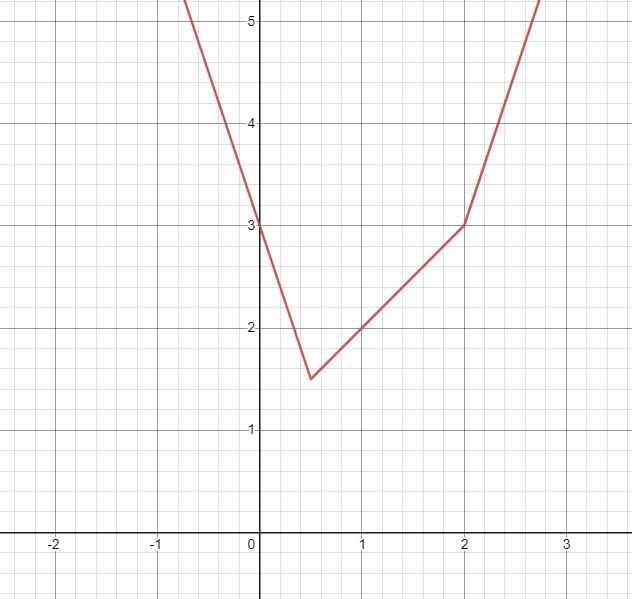
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)
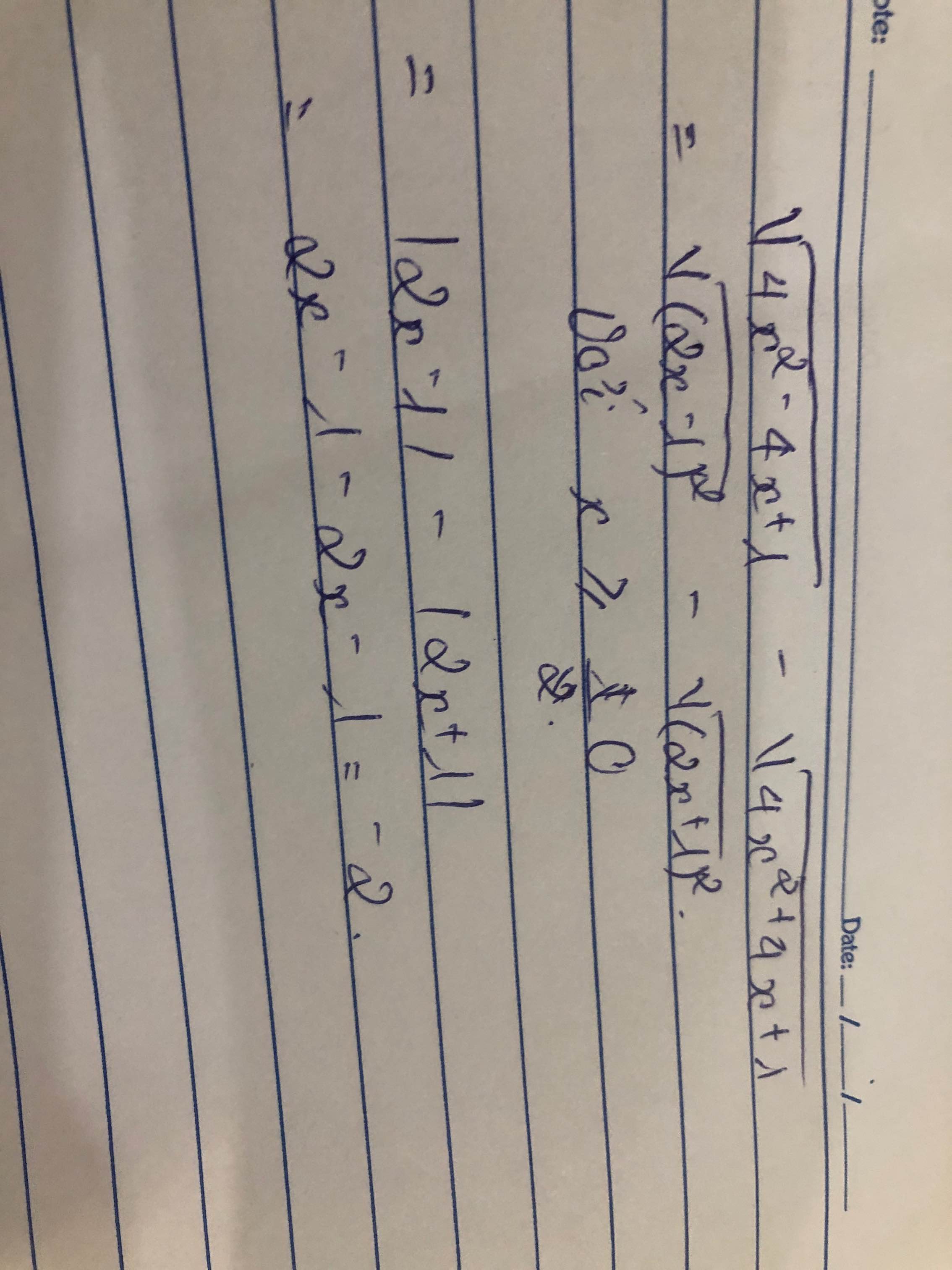
4x+2 + 2.4x = 288
\(\Rightarrow\) 4x (42 + 2) = 288
\(\Rightarrow\) 4x.18 = 288
\(\Rightarrow\) 4x = 16
\(\Rightarrow\) x = 2
Vậy x =2.