Cho tamgiasc ABC vuông ở A, đường cao AH. Gọi M, N theo thứ tự là trung điểm của AB, AC. Biết HM = 15cm, HN = 20cm. Tính HB, HC, AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


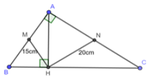
Xét ∆ ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = 1 2 AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ∆ ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = 1 2 AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
![]()
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D

tam giác AHB vuông tại H có HM là trung tuyến ứng với cạnh huyền AB=> HM=1/2AB=>AB=2HM=2.15=30cm
tam giác AHC vuông tại H có HN là trung tuyến ứng với cạnh huyền AC=>HN=1/2AC=>AC=2HN=2.20=40 cm
tam giác ABC vuông tại A =>\(BC^2=AB^2+AC^2suyraBC=\sqrt{AB^2+AC^2}=\sqrt{30^2+40^2}=50cm\)
ta có AH.BC=AB.AC=>AH=[30.40]/50=24cm hệ thức lượng tam giác vuông
ta có \(AB^2=BH.BCsuyraBH=\frac{AB^2}{BC}=\frac{30^2}{50}=18cm\)
suy ra HC=BC-BH=50-18=32cm

Vì M là trung điểm của AB => HM là trung tuyến
Mà \(\Delta ABH\)vuông tại H
=> \(HM=\frac{1}{2}AB\)( trong tam giác vuông trung tuyến ứng với cạnh huyền = 1 phần 2 cạnh huyền )
=> AB = 30 cm
Chứng minh tương tự
=> AC= 40 cm
Xét \(\Delta ABC\)có ( A = 900 )
=> \(BC=\sqrt{AC^2+AB^2}=50\)cm
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Rightarrow\frac{1}{AH}=\sqrt{\frac{1}{AB^2}+\frac{1}{AC^2}}=\frac{1}{24}\)
\(\Rightarrow AH=24cm\)
Áp dụng hệ thức cạnh trong tam giác vuông ta có :
\(AB^2=BH.BC\)
\(\Rightarrow BH=AB^2:BC=18cm\)
Vì BH + HC = BC
\(\Rightarrow HC=50-18=32cm\)
Study well

a) Cm. AH = DE
Ta có: HD vuông góc với BA (gt)
ED vuông góc với BA ( BA vuông góc với AC; E thuộc AC)
=> HD // EA
Ta lại có: DA vuông góc với AC ( BA vuông góc với AC; D thuộc AB)
HE vuông góc với AC (gt)
=> DA // HE
Xét tứ giác DHEA, có;
* HD // EA (cmt)
* DA // HE (cmt)
=> DHEA là hình bình hành (định nghĩa)
=> DE = AH (tính chất của đường chéo) (đpcm)
b) Gọi O là giao điểm của 2 đường chéo DE, AH của hình bình hành DHEA.
Xét tam giác HEC vuông tại E, có:
* K là trung điểm của HC (gt)
=> EK = KH = KC (trung tuyến của tam giác vuông bằng 1/2 cạnh huyền)
=> DI = IH = IB ( chứng minh tương tự)
Xét tam giác DIO và tam giác HIO, có:
* DI = IH (cmt)
* IO là cạnh chung
* OD = OH (DHEA là hình bình hành)
=> tam giác DIO = tam giác HIO (c.c.c)
=> góc IHO = góc IDO ( yếu tố tương ứng)
Mà góc IHO = 90 độ (AH là đường cao)
=> góc IDO = 90 độ
=> ID vuông góc với DE (1)
Xét tam giác HOK và tam giác EOK, có:
* HO = EO (DHEA là hình bình hành)
* OK là cạnh chung
* KH = KE (cmt)
=> tam giác HOK = tam giác EOK (c.c.c)
=> góc OHK = góc OEK ( yếu tố tương ứng)
Mà góc OHK = 90 độ (AH là đường cao)
=> góc OEK = 90 độ
=> KE vuông góc với DE (2)
Từ (1), (2) => ID // KE (từ vuông góc đến song song) (đpcm).

a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC hay MN//EF
Suy ra MNEF là hthang
Lại có \(MN=\dfrac{1}{2}BC\) và \(EF=EH+HF=\dfrac{1}{2}\left(BH+HC\right)=\dfrac{1}{2}BC\)
Do đó MNEF là hbh
Lại có ME là đtb tg ABH nên ME//AH
Mà AH⊥BC và MN//BC nên ME⊥MN
Vậy MNEF là hcn

Tam giác AHB vuông tại H có HM là trung tuyến
=> HM = 1/2 AB => AB = 30 cm
Tam giác AHC vuông tại H có HN là trung tuyến
=> HN = 1/2 AC => AC = 40 cm
Áp dụng Pytago ta có: AB2 + AC2 = BC2
=> BC2 = 302 + 402 = 2500
=> BC = 50
Áp dụng hệ thức lượng ta có:
AB2 = BH.BC => \(BH=\frac{AB^2}{BC}=18\)
AC2 = CH.BC => \(CH=\frac{AC^2}{BC}=32\)
HA.BC = AB.AC => \(HA=\frac{AB.AC}{BC}=24\)

a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{AEH}=\widehat{ADH}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=15^2+20^2=625\)
hay BC=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot25=15\cdot20\)
\(\Leftrightarrow AH\cdot25=300\)
hay AH=12(cm)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Vậy: BC=20cm; AH=12cm; HC=16cm
Xét tg ABH vuông tại H có Ma=MB=> MH là đường trung tuyến
=>MH=\(\frac{1}{2}\)AB=>AB=30cm
Xét tg AHC vuông tại H có AN=NC=>HN là đường trung tuyến
=>HN=\(\frac{1}{2}\)AC=>AC=40cm
Xét tg ABC vuông tại A có:
BC2=AB2+AC2(py-ta-go)
=>BC=50cm
Xét tg ABC có góc A=90o,đg cao AH ứng vs cạnh huyền BC.Aps dụng HTL tro tg vuông ta có:
AB2=BC.BH=>BH=18cm
Lại có:AC2=HC.BC=>HC=32cm
AH2=BH.HC =>AH=24cm