Giải PT \(\sqrt{2x-3}-\sqrt{x}=2x-6\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
T
12 tháng 3 2021
ĐKXĐ: \(-3\le x\le6\)
Trước hết ta chứng minh:
\(\sqrt{x+3}+\sqrt{6-x}\le3\sqrt{2}\)
Mặt khác điều này hiển nhiên do bất đẳng thức Bunyakovski:
\(VT\le\sqrt{2\left[\left(x+3\right)+\left(6-x\right)\right]}=3\sqrt{2}\)
Đẳng thức xảy ra khi \(x+3=6-x\Leftrightarrow x=\dfrac{3}{2}\)
Mặt khác theo AM-GM:
\(6\sqrt{2x+6}-2x-13=2\sqrt{9\left(2x+6\right)}-2x-13\le\left[9+\left(2x+6\right)\right]-2x-13=2\)
Đẳng thức xảy ra khi $x=\dfrac{3}{2}.$
Từ đây thu được \(VT\le VP.\)
Đẳng thức xảy ra khi $x=\dfrac{3}{2}.$
Vậy \(S=\left\{\dfrac{3}{2}\right\}\)
30 tháng 11 2021
ĐKXĐ:\(\left\{{}\begin{matrix}2x-3\ge0\\x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x\ge0\end{matrix}\right.\Rightarrow x\ge\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x}=2x-6\\ \Leftrightarrow\dfrac{2x-3-x}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\\ \Leftrightarrow\dfrac{x-3}{\sqrt{2x-3}+\sqrt{x}}-2\left(x-3\right)=0\\ \Leftrightarrow\left(x-3\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}-2=0\end{matrix}\right.\)
Với \(x-3=0\Rightarrow x=3\left(tm\right)\)
\(Với\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}-2=0\\ \Leftrightarrow\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}=2\\ \Leftrightarrow2\sqrt{2x-3}+2\sqrt{x}=1\left(đến.đây.bạn.cm.nó,vô.nghiệm.nhé\right)\)
DT
1
28 tháng 11 2021
a, ĐKXĐ: ...
\(\sqrt{3x^2-2x+6}+3-2x=0\)
\(\Leftrightarrow\sqrt{3x^2-2x+6}=2x-3\)
\(\Leftrightarrow3x^2-2x+6=4x^2-12x+9\)
\(\Leftrightarrow4x^2-10x+3=0\)
.....
b, ĐKXĐ: ...
\(\sqrt{x+1}+\sqrt{x-1}=4\\ \Leftrightarrow x+1+x-1+2\sqrt{\left(x+1\right)\left(x-1\right)}=16\\ \Leftrightarrow2\sqrt{x^2-1}=16-2x\\ \Leftrightarrow\sqrt{x^2-1}=8-x\\ \Leftrightarrow x^2-1=64-16x+x^2\\ \Leftrightarrow65-16x=0\\ \Leftrightarrow x=\dfrac{65}{16}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 4 2021
a.
ĐKXĐ: \(1\le x\le7\)
\(\Leftrightarrow x-1-2\sqrt{x-1}+2\sqrt{7-x}-\sqrt{\left(x-1\right)\left(7-x\right)}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(\sqrt{x-1}-2\right)-\sqrt{7-x}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-1}-\sqrt{7-x}\right)\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=\sqrt{7-x}\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=7-x\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 4 2021
b. ĐKXĐ: ...
Biến đổi pt đầu:
\(x\left(y-1\right)-\left(y-1\right)^2=\sqrt{y-1}-\sqrt{x}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x}=a\ge0\\\sqrt{y-1}=b\ge0\end{matrix}\right.\)
\(\Rightarrow a^2b^2-b^4=b-a\)
\(\Leftrightarrow b^2\left(a+b\right)\left(a-b\right)+a-b=0\)
\(\Leftrightarrow\left(a-b\right)\left(b^2\left(a+b\right)+1\right)=0\)
\(\Leftrightarrow a=b\)
\(\Leftrightarrow\sqrt{x}=\sqrt{y-1}\Rightarrow y=x+1\)
Thế vào pt dưới:
\(3\sqrt{5-x}+3\sqrt{5x-4}=2x+7\)
\(\Leftrightarrow3\left(x-\sqrt{5x-4}\right)+7-x-3\sqrt{5-x}=0\)
\(\Leftrightarrow\dfrac{3\left(x^2-5x+4\right)}{x+\sqrt{5x-4}}+\dfrac{x^2-5x+4}{7-x+3\sqrt{5-x}}=0\)
\(\Leftrightarrow\left(x^2-5x+4\right)\left(\dfrac{3}{x+\sqrt{5x-4}}+\dfrac{1}{7-x+3\sqrt{5-x}}\right)=0\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
ĐKXĐ: \(0\le x\le5\)
Pt tương đương:
\(\sqrt{x+3}+4\sqrt{x}+\sqrt{5-x}=2x+6\)
Ta có:
\(VT=\dfrac{1}{2}.2.\sqrt{x+3}+4.1.\sqrt{x}+\dfrac{1}{2}.2.\sqrt{5-x}\)
\(VT\le\dfrac{1}{4}\left(4+x+3\right)+2\left(1+x\right)+\dfrac{1}{4}\left(4+5-x\right)\)
\(\Rightarrow VT\le2x+6=VP\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{x}=1\\\sqrt{5-x}=2\end{matrix}\right.\) \(\Leftrightarrow x=1\)
9 tháng 11 2022
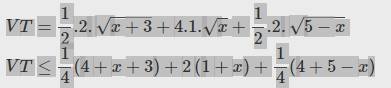
Từ bước trên xuống bước dưới áp dụng công thức nào vậy thầy - Nhờ thầy chỉ rõ hơn.
Trân trọng!
DT
0
14 tháng 12 2020
a, \(\sqrt{2x^2-3}=\sqrt{4x-3}\) (x \(\ge\) \(\sqrt{\dfrac{3}{2}}\))
Vì hai vế ko âm, bp 2 vế ta được:
2x2 - 3 = 4x - 3
\(\Leftrightarrow\) 2x2 = 4x
\(\Leftrightarrow\) x2 = 2x
\(\Leftrightarrow\) x2 - 2x = 0
\(\Leftrightarrow\) x(x - 2) = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(KTM\right)\\x=2\left(TM\right)\end{matrix}\right.\)
Vậy S = {2}
b, \(\sqrt{2x-1}=\sqrt{x-1}\) (x \(\ge\) 1)
Vì hai vế ko âm, bp 2 vế ta được:
2x - 1 = x - 1
\(\Leftrightarrow\) x = 0 (KTM)
Vậy x = \(\varnothing\)
c, \(\sqrt{x^2-x-6}=\sqrt{x-3}\) (x \(\ge\) 3)
Vì hai vế ko âm, bp 2 vế ta được:
x2 - x - 6 = x - 3
\(\Leftrightarrow\) x2 - 2x - 3 = 0
\(\Leftrightarrow\) x2 - 3x + x - 3 = 0
\(\Leftrightarrow\) x(x - 3) + (x - 3) = 0
\(\Leftrightarrow\) (x - 3)(x + 1) = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(TM\right)\\x=-1\left(KTM\right)\end{matrix}\right.\)
Vậy S = {3}
d, \(\sqrt{x^2-x}=\sqrt{3x-5}\) (x \(\ge\) \(\dfrac{5}{3}\))
Vì hai vế ko âm, bp 2 vế ta được:
x2 - x = 3x - 5
\(\Leftrightarrow\) x2 - 4x + 5 = 0
\(\Leftrightarrow\) x2 - 4x + 4 + 1 = 0
\(\Leftrightarrow\) (x - 2)2 + 1 = 0
Vì (x - 2)2 \(\ge\) 0 với mọi x \(\ge\) \(\dfrac{5}{3}\) \(\Rightarrow\) (x - 2)2 + 1 > 0 với mọi x \(\ge\) \(\dfrac{5}{3}\)
\(\Rightarrow\) Pt vô nghiệm
Vậy S = \(\varnothing\)
Chúc bn học tốt!
20 tháng 3 2016
Điều kiện với \(x\ge\frac{3}{2}.\) Khi đó PT đã cho tương đương với:
\(\frac{\left(\sqrt{2x-3}-\sqrt{x}\right)\left(\sqrt{2x-3}+\sqrt{x}\right)}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\)
\(\Leftrightarrow\frac{x-3}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\)
\(\Leftrightarrow\) hoặc x = 3 ( thỏa mãn ) hoặc
\(2-\frac{1}{\sqrt{2x-3}+\sqrt{x}}=0\) ( 1 )
Từ điều kiện \(x\ge\frac{3}{2}\) suy ra \(2-\frac{1}{\sqrt{2x-3}+\sqrt{x}}\ge0\)
Do đó PT 1 vô nghiệm.
Vậy PT đã cho có nghiệm duy nhất x = 3.
@@
Điều kiện \(x\ge\dfrac{3}{2}\). Khi đó pt đã cho tương đương với:
\(\dfrac{\left(\sqrt{2x-3}-\sqrt{x}\right)\left(\sqrt{2x-3}+\sqrt{x}\right)}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{\sqrt{2x-3}+\sqrt{x}}=2\left(x-3\right)\)
\(\Leftrightarrow\) hoặc x = 3 ( thỏa mãn ) hoặc \(2-\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}=0\left(1\right)\)
Từ ĐK \(x\ge\dfrac{3}{2}>1\Rightarrow2-\dfrac{1}{\sqrt{2x-3}+\sqrt{x}}>0\)
Do đó PT ( 1 ) vô nghiệm.
Vậy PT đã cho có nghiệm duy nhất x = 3.