Cho tam giác ABC có ba đường cao lần lượt là 3,6 ; 4,5 ; 6
tính diện tích tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử a; b; c lần lượt là các cạnh của tam giác ABC ứng với 3 đường cao ha = 3,6; hb = 4,5; hc = 6 (a = BC; b = AC; c = AB)
Ta có a.ha = b.hb = c.hc (cùng bằng 2.SABC)
=> 3,6.a = 4,5.b = 6.c => 36a = 45b = 60c => \(\frac{36a}{180}=\frac{45b}{180}=\frac{60c}{180}\) => \(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}\)
Đặt \(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}=k\) ( k khác 0) => a = 5k; b = 4k ; c = 3k
Nhận xét: (4k)2 + (3k)2 = (5k)2 => b2 + c2 = a2 => Tam giác ABC vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông ABC có: AH.BC = AB . AC => 3,6.5k = 3k.4k => 12k2 = 18k => k = 18/12 = 1,5
=> BC = 5k = 5.1,5 = 7,5
=> S(ABC) = AH.BC /2 = 3,6.7,5: 2 = 13,5

a: ha=9; hb=12; hc=16
=>hc*9=ha*16=hb*12
=>hc/16=ha/9=hb/12
=>Haitam giác này đồng dạng
b: ha=4; hb=5; hc=6
=>ha*6=24; hb*5=25; ha*4=24
=>Hai tam giác này ko đồng dạng

hình như dựa vào tính chất dãy tỉ số bằng nhau ak pn. mk cx chỉ nhớ z thui chứ hk chắc cko lém :)

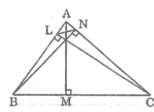
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)

Lời giải:
a/ Tứ giác $AEHF$ có 3 góc vuông: $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hình chữ nhật.
$\Rightarrow AH=EF$
b/ $HF=AE$ (do $AEHF$ là hcn)
Xét tam giác $AEH$ và $AHB$ có:
$\widehat{A}$ chung
$\widehat{AEH}=\widehat{AHB}=90^0$
$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)
$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$
$\Rightarrow AE=\frac{AH^2}{AB}=\frac{AB^2-BH^2}{AB}=\frac{6^2-3,6^2}{6}=3,84$ (cm)

a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE