y=x3+mx2+nx+3m+2 đạt giá trị cực tiểu =4 khi x=-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 9 2018
Đáp án B
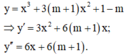
Hàm số đạt cực tiểu tại x = -1 khi và chỉ khi
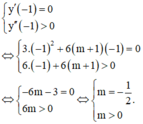
Vậy không có giá trị nào của m thỏa mãn đề bài.
CM
27 tháng 2 2018
Đáp án B
Kiến thức cần nhớ: Cho hàm số y=f(x) có đạo hàm cấp một trên (a;b) chứa điểm x 0 và y=f(x) có đạo hàm cấp hai khác 0 tại x 0 , khi đó:
CM
13 tháng 8 2018
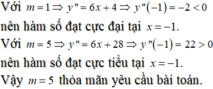
Đáp án C
Ta có y ' = 3 x 2 − 2 m x + 2 m − 3
Hàm số đạt cực đại tại x = 1 ⇒ y ' 1 = 0 ⇔ 3 − 2 m + 2 m − 3 = 0 ⇒ ∀ m ∈ ℝ
Ta có y " = 6 x − 2 m ⇒ y " 1 = 6 − 2 m < 0 ⇒ m > 3
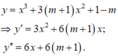
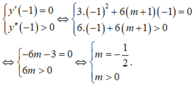
Lời giải:
Hàm \(y=x^3+mx^2+nx+3m+2\) đạt cực tiểu khi $x=-1$ thì phương trình \(y'=3x^2+2mx+n=0\) nhận \(x=-1\) là nghiệm
\(\Rightarrow 3-2m+n=0(1)\)
Mặt khác
\(y(-1)=-1+m-n+3m+2=1+4m-n=4\Leftrightarrow 4m-n=3(2)\)
Từ \((1),(2)\Rightarrow \)\(\left\{\begin{matrix} m=0\\ n=-3\end{matrix}\right.\)
y =x^3 +mx^2 +nx +3m +2
y' =3x^2 +2mx +n
y''=6x +2mx +n
(đk1)f' (-1) =0 => 3.(-1)^2+2m.(-1) +n =0 <=> 2m -n-3 =0
(đk2).D= m^2 -3n>0
(đk 3) f''(-1) >0 => 6.(-1) +2m(-1) +n>0
(dk4) f(-1) =4 => -1 +m-n+3m+2 =4
<=> hệ
2m -n-3 =0 (1)
m^2 -3n>0 (2)
2m -n +6<0 (3)
4m -n +1 =4 (4)
từ (1) và (4) 2m =6 => m =0; n =-3
thay vào (2) => -3.(-3) >0 nhận
thay vào (3) => 3+6 =>0 => loại
kết luận không có m,n thỏa mãn.