BT: Với góc nhọn \(\alpha\) \(\left(0^o<\alpha<90^o\right)\), CMR : \(\frac{1}{\sin^2\alpha}=\frac{1}{\tan^2\alpha}+1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2021
Câu 1:
Ta có: \(\cos\left(90^0-\alpha\right)=\sin\alpha\)
\(\Leftrightarrow\sin\alpha=1:\sqrt{\dfrac{1^2+2^2}{1}}=1:\sqrt{5}=\dfrac{\sqrt{5}}{5}\)
Câu 2:
a) \(\cos\alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-\dfrac{16}{25}}=\dfrac{3}{5}\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
9 tháng 1 2017
Câu 2 đề sai, phải là tìm \(max\) bạn nhé.
Đặt \(a=\sin x,b=\cos x\) thì \(P\left(x\right)=3a+\sqrt{3}b\) với \(a^2+b^2=1\)
(Tư tưởng Cauchy-Schwarz quá rõ)
Ta có \(\left(a^2+b^2\right)\left(9+3\right)\ge\left(3a+\sqrt{3}b\right)^2=P^2\left(x\right)\)
Suy ra \(P\left(x\right)\le2\sqrt{3}\). Đẳng thức xảy ra tại \(x=60\) độ.
Câu 1 để mình suy nghĩ sau.
AD
25 tháng 7 2023
\(\dfrac{\left(sina+cosa\right)^2-\left(sina-cosa\right)^2}{sina.cosa}=4\\ VT=\dfrac{sin^2a+2sinacosa+cos^2a-sin^2a+2sinacosa-cos^2a}{sinacosa}\\ =\dfrac{4sinacosa}{sinacosa}=4=VP\)
25 tháng 7 2023
a: \(S=cos^2a\left(1+tan^2a\right)=cos^2a\cdot\dfrac{1}{cos^2a}=1\)
b: \(VP=\dfrac{1+sin2a-1+sin2a}{\dfrac{1}{2}\cdot sin2a}=\dfrac{2\cdot sin2a}{\dfrac{1}{2}\cdot sin2a}=4=VT\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
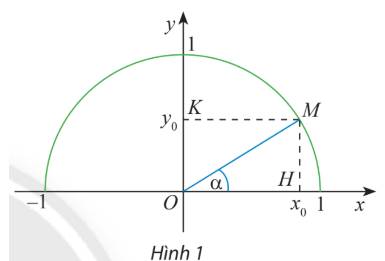
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
A
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(cot^2a=\left(\dfrac{a^2-b^2}{2ab}\right)^2\Leftrightarrow\dfrac{cos^2a}{sin^2a}=\dfrac{a^4+b^4-2a^2b^2}{4a^2b^2}\)
\(\Leftrightarrow\dfrac{cos^2a}{sin^2a}+1=\dfrac{a^4+b^4-2a^2b^2}{4a^2b^2}+1\)
\(\Leftrightarrow\dfrac{1}{sin^2a}=\dfrac{a^4+b^4+2a^2b^2}{4a^2b^2}\)
\(\Leftrightarrow sin^2a=\dfrac{4a^2b^2}{a^4+b^4+2a^2b^2}\)
\(\Leftrightarrow cos^2a=1-sin^2a=1-\dfrac{4a^2b^2}{a^4+b^4+2a^2b^2}=\dfrac{a^4+b^4-2a^2b^2}{a^4+b^4+2a^2b^2}\)
\(\Leftrightarrow cos^2a=\left(\dfrac{a^2-b^2}{a^2+b^2}\right)^2\)
\(\Leftrightarrow cosa=\dfrac{a^2-b^2}{a^2+b^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
Nhìn sự khác nhau giữa dòng 2 và dòng 3 và tự suy luận đi em, rất đơn giản đúng ko?
Xét tam giác ABC vuông tại A có BC = a; AC = b; AB = c và góc B \(=\alpha\) .
Bạn tự vẽ hình nha. CM: Ta có:
\(\frac{1}{\tan^2\alpha}+1=\frac{1}{\frac{b^2}{c^2}}+1=\frac{c^2}{b^2}+1=\frac{c^2+b^2}{b^2}=\frac{a^2}{b^2}\) (định lí Py-ta-go)
\(\frac{1}{\sin^2\alpha}=\frac{1}{\frac{b^2}{a^2}}=\frac{a^2}{b^2}\). Do đó: \(\frac{1}{\sin^2\alpha}=\frac{1}{\tan^2\alpha}+1\)