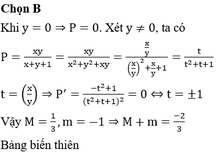Cho đa thức M = x2+y2 = xy. Tìm x, y sao cho giá trị của M nhỏ nhất biết x + y = 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)
CM
19 tháng 12 2017
Ta có m − 1 x − m y = 3 m − 1 2 x − y = m + 5 ⇔ y = 2 x − m − 5 m − 1 x − m 2 x − m − 5 = 3 m − 1
⇔ y = 2 x − m − 5 m − 1 x − 2 m x + m 2 + 5 m = 3 m − 1 ⇔ y = 2 x − m − 5 − m − 1 x = − m 2 − 5 m + 3 m − 1 ⇔ y = 2 x − m − 5 m + 1 x = m 2 + 2 m + 1 ⇔ y = 2 x − m − 5 1 m + 1 x = m + 1 2 2
Để hệ phương trình có nghiệm duy nhất thì phương trình (2) có nghiệm duy nhất hay m ≠ − 1
Khi đó từ phương trình (2) ta suy ra x = m + 1 2 m + 1 = m + 1 , thay x = m + 1vào phương trình (1) ta được y = 2 (m + 1) – m – 5 = m – 3
Vậy với m ≠ − 1 thì hệ đã cho có nghiệm duy nhất (x; y) = (m + 1; m – 3)
Ta xét S = x 2 + y 2 = ( m + 1 ) 2 + ( m – 3 ) 2 = m 2 + 2 m + 1 + m 2 − 6 m + 9
= 2 m 2 – 4 m + 10 = 2 ( m 2 – 2 m + 1 ) + 8 = 2 ( m – 1 ) 2 + 8
Vì ( m – 1 ) 2 ≥ 0 ; ∀ m ⇒ 2 ( m – 1 ) 2 + 8 ≥ 8 ; ∀ m
Hay S ≥ 8 ; ∀ m . Dấu “=” xảy ra khi m–1 = 0 ⇔ m=1 (TM)
Vậy m = 1 là giá trị cần tìm
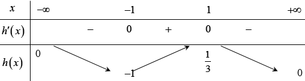
Đáp án: A
CM
15 tháng 3 2018
Ta có: 2 x 2 + 1 2 ≥ 2 x ; 2 y 2 + 1 2 ≥ 2 y và x 2 + y 2 ≥ 2 x y
Cộng vế với vế các BĐT trên ta được:
3 x 2 + y 2 + 1 ≥ 2 x + y + x y = 5 2
=> A = x 2 + y 2 ≥ 1 2
Từ đó tìm được A m i n = 1 2 <=> x = y = 1 2
V
1
DH
18 tháng 4 2021
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
21 tháng 12 2021
\(M=x^3+x^2y-2x^2-xy-y^2+3y+x+2017\)
\(\Rightarrow M=\left(x^3+x^2y-2x^2\right)-xy-y^2+2y+y+x-2+2019\)
\(\Rightarrow M=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+\left(y+x-2\right)+2019\)
\(\Rightarrow M=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+2019\)
\(\Rightarrow M=\left(x^2-y+1\right)\left(x+y-2\right)+2019\)
\(\Rightarrow M=\left(x^2-y+1\right).0+2019\)
\(\Rightarrow M=0+2019\)
\(\Rightarrow M=2019\)