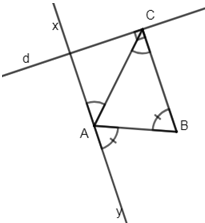
Cho hình vẽ, biết Ax//By và \(\widehat{CBy}\) \(>\widehat{ACB.}\) Chứng minh rằng \(\widehat{yBC}\)\(=\widehat{xAC}\)\(+\widehat{ACB}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 5 2022
`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`
CS
6 tháng 10 2021
a) Ta có: CD//Ey
\(\Rightarrow\widehat{CBE}=\widehat{E_1}=130^0\)(so le trong)
b) Ta có: Ta có: CD//Ey
\(\Rightarrow\widehat{EBD}+\widehat{E_1}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{EBD}=180^0-\widehat{E_1}=50^0\)
Ta có: \(\widehat{EBD}+\widehat{B_1}=50^0+40^0=90^0\)
=> AB⊥BE
NX
9 tháng 8 2023
a) Ta có: mà hai góc đó là hai góc so le trong nên
suy ra (1)
mà hai góc đó là hai góc so le trong nên suy ra (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà và
nên suy ra
Mà nên suy ra
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền - cạnh góc vuông) nên \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng)
Gọi By' là tia đối của tia By.
Gọi I là giao điểm của AC và yy'
By//Ax (gt) nên By'//Ax
Do By'//Ax nên xAC=AIy' ( so le trong)
Ta lại có: AIy=BIC ( đối đỉnh)
Do yBC là góc ngoài tại đỉnh B của tam giác BCI nên:
yBC=BIC+ACB
Mà xAC=AIy'
BIC=AIy'
=> xAC=BIC
Do đó yBC=xAC+ACB (đpcm)